Khoa Sư phạm

           Sử dụng tô pô, một chuyên ngành toán học nghiên cứu các tính chất không thay đổi của vật thể khi bị biến dạng liên tục, như một công cụ, ba nhà khoa học đoạt giải Nobel Vật lý năm nay đã “khám phá được bí mật của các vật chất lạ”, “làm cho các chuyên gia phải sững sờ”.

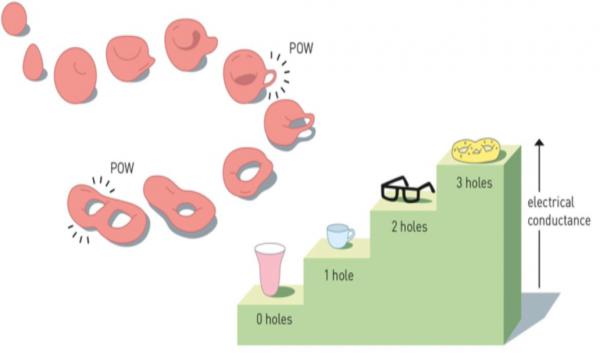
Biến một cái cốc thành hình xuyến nhờ các phép biến đổi liên tục tô pô.

Giải Nobel Vật lý 2016 vừa được trao cho ba nhà vật lý lý thuyết David Thouless (Đại học Washington), Duncan Haldane (Đại học Princeton) và Michael Kosterlitz (Đại học Brown) về “những phát minh lý thuyết về sự dịch chuyển các trạng thái tô pô và các trạng thái tô pô của vật chất” (trích thông báo của Viện Hàn lâm khoa học Thụy Điển). Thouless được nửa giải, còn Haldane và Kosterlitz chia nhau nửa giải còn lại.
     “Những người đoạt giải Nobel năm nay đã mở cửa một thế giới bí ẩn mà trong đó vật chất có thể nhận những trạng thái kỳ lạ. Họ đã sử dụng các phương pháp toán học tiên tiến để nghiên cứu các giai đoạn hay trạng thái không bình thường của vật chất như các chất siêu dẫn, siêu lỏng hoặc màng từ mỏng.” “Việc sử dụng các khái niệm tô pô của ba người đoạt giải Nobel trong vật lý là yếu tố quyết định đối với những phát minh của họ.”
     Tô pô là một chuyên ngành toán học nghiên cứu các tính chất không thay đổi của vật thể khi bị biến dạng một cách liên tục. Hai vật thể được coi là giống nhau về tô pô nếu có thể bóp nặn hay kéo giãn một vật này thành vật kia, ví dụ như một cái cốc có tay cầm và một cái vòng. Chúng có tính chất tô pô chung là chỉ chứa một lỗ hổng. Có thể phân biệt đặc tính tô pô của các vật thể thông qua số lỗ hổng của chúng. Khó có thể hình dung được chuyên ngành toán học trừu tượng này lại tìm thấy ứng dụng trong thực tiễn. Sử dụng tô pô như một công cụ, ba người đoạt giải Nobel năm nay đã “khám phá được bí mật của các vật chất lạ”, “làm cho các chuyên gia phải sững sờ”.
       Thông thường, vật chất có ba trạng thái rắn, lỏng và khí. Khi nhiệt độ thay đổi, chúng sẽ thay đổi trạng thái giống như nước bốc hơi khi sôi và đóng băng ở nhiệt độ âm. Các sự dịch chuyển trạng thái có thể giải thích được bằng sự chuyển động giữa các nguyên tử. Các nguyên tử sẽ tương tác với nhau theo các quy luật của vật lý lượng tử. Tuy nhiên, khi vật chất có dạng màng cực mỏng, sẽ xảy ra các hiện tượng khó hiểu. Ở nhiệt độ thấp, các nguyên tử của chúng có thể chuyển động mà không cản trở lẫn nhau nữa. Ví dụ như ta có hiện tượng siêu dẫn khi dòng điện được truyền tải mà không bị tiêu hao điện năng. Truyền tải trên các đường dây điện thông thường sẽ mất khoảng 15-20% điện năng. Vì vậy nếu dùng chất siêu dẫn thì sẽ tiết kiệm được rất nhiều chi phí. Tương tự như vậy là các chất siêu lỏng không chịu sự tác động của lực ma sát, có thể chuyển động mãi mãi.
         Đầu những năm1970, Michael Kosterlitz và David Thouless lật ngược các lý thuyết trước đó cho rằng không thể xảy ra sự dịch chuyển trạng thái trong các màng mỏng. Họ đưa ra khái niệm các vùng xoáy để giải thích hiện tượng siêu dẫn ở nhiệt độ thấp và cơ chế chuyển pha (giai đoạn) làm cho tính siêu dẫn biến mất ở nhiệt độ cao hơn. Các vùng xoáy là những cấu hình tô pô ổn định. Ở nhiệt độ thấp, chúng gắn chặt theo từng đôi; nhưng ở nhiệt độ cao, chúng sẽ rời nhau ra và chuyển động tự do. Mô hình dịch chuyển của Kosterlitz và Thouless được coi là một trong những phát minh quan trọng nhất của thế kỷ 20 trong ngành Vật lý chất rắn. Nó còn được áp dụng để giải thích một số hiện tượng trong Vật lý nguyên tử và Cơ học thống kê.
         Trong những năm 1980, Thouless giải thích được hiệu ứng Hall lượng tử xảy ra đối với các màng mỏng bán dẫn ở nhiệt độ cực thấp, trong đó độ dẫn điện thay đổi theo bậc số nguyên. Trước đó người ta không hiểu được tại sao độ dẫn điện lại thay đổi không liên tục mà lại theo cấp số nguyên. Thouless đã chỉ ra rằng hiệu ứng này mang tính tô pô. Xét về phương diện tô pô, vật thể sẽ thay đổi khi có thêm lỗ hổng và độ dẫn điện chỉ phụ thuộc vào số lỗ hổng.
          Cũng trong những năm 1980, Haldane phát hiện thấy khái niệm tô pô có thể sử dụng để giải thích tính chất của những chuỗi hạt nam châm được tìm thấy trong một số vật liệu. Các chuỗi hạt nam châm này có những đặc tính hoàn toàn khác biệt phụ thuộc vào tính chẵn lẻ của nam châm nguyên tử. Haldane chứng minh rằng nam châm chẵn có tính tô pô, còn nam châm lẻ thì không. Điều này lý giải tại sao chúng có những thuộc tính khác nhau hoàn toàn.

Minh hoạ về tô pô

Bây giờ chúng ta biết rất nhiều những sự dịch chuyển trạng thái tô pô, không chỉ trong các đường và màng mỏng hai chiều mà còn trong các vật liệu ba chiều thông thường. Trong thập kỷ qua, các phát minh của Thouless, Haldane và Kosterlitz đã thúc đẩy mạnh mẽ các nghiên cứu hàng đầu trong ngành vật lý chất rắn nhằm tìm ra các vật chất lạ. Người ta hy vọng các vật liệu này có thể được sử dụng trong các thế hệ thiết bị điện tử và vật liệu siêu dẫn mới, hoặc trong các máy tính lượng tử tương lai.

GS. Ngô Việt Trung

                                                                            (Bài đã đăng trên Tia sáng năm 2016)

                                 Một  minh họa giữa Toán học và Vật Lý

                  Chứng minh công thức Euler cho đa diện bằng vật lý

         Giải Nobel vật lý năm nay được trao cho ba nhà vật lý, Thouless, Haldane và Kosterlitz, vì những đóng góp liên quan đến các chuyển pha và các trạng thái tôpô. Nhân dịp này chúng ta sẽ dùng vật lý để chứng minh một công thức khá nổi tiếng, liên quan đến tôpô – công thức Euler cho đa diện. Công thức này nói rằng với một đa diện bất kỳ, số đỉnh V, số mặt F và số cạnh E của nó thoả mãn

                                              V + F – E = 2.

     Ví dụ với hình lập phương ta có V = 8, F = 6, E = 12, và 8 + 6 – 12 = 2. Bạn có thể kiểm tra với một vài hình đa diện nữa để thấy công thức luôn đúng.

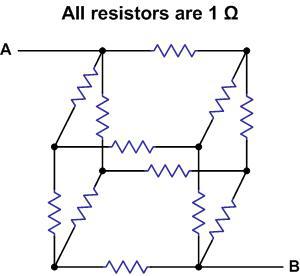
Để chứng minh công thức này, ta sẽ lắp một mạch điện theo hình đa diện, thay mỗi cạnh của đa diện bằng một điện trở. Không quan trọng lắm các giá trị của điện trở là bao nhiêu, miễn là tất cả các điện trở đều khác không. Để cho đơn giản ta cho mỗi điện trở là 1 Ω. Sau đó ta chọn hai đỉnh và nối hai cực của một nguồn điện vào hai đỉnh đó, cũng không quan trọng lắm là đỉnh nào. Chẳng hạn với hình lập phương ta có thể tưởng tượng ra mạch điện như sau:

Khi ta nối một mạch điện như vậy, tất nhiên điện sẽ chạy trong mạch một cách nhất định. Ta có thể đặt nhiều câu hỏi với mạch điện này. Ví dụ ta có thể hỏi điện trở của mạch là bao nhiêu. Câu hỏi tôi sẽ hỏi là như sau: giả sử tổng dòng điện chạy qua mạch là 1 Amper, dòng điện chạy qua từng điện trở là bao nhiêu? (Tất nhiên là nếu trả lời được câu hỏi này thì có thể tìm ra được điện trở của mạch).

Để trả lời câu hỏi trên, ta sẽ lập một hệ phương trình cho phép ta tìm được dòng điện chảy qua từng điện trở. Giả sử AB là một cạnh, ta ký hiệu IAB là dòng điện chạy từ đỉnh A đến đỉnh B. Ta có IAB = –IBA, và có tổng cộng E đại lượng này. Ta sẽ lập một hệ phương trình để tìm giá trị của các dòng điện này.

Có hai loại phương trình, xuất phát từ hai định luật Kirchhoff. Loại đầu tiên là như sau. Giả sử A là một đỉnh, và B, C, D… là các đỉnh kề A. Ta có phương trình:

IAB + IAC + IAD + … = 0 hoặc 1 hoặc –1.

Vế phải là 0 nếu như đỉnh A không phải một trong hai đỉnh nối vào nguồn điện, là 1 nếu A được nối vào cực dương và –1 nếu A nối vào cực âm. Đơn giản phương trình này nói dòng điện chạy vào một đỉnh phải bằng dòng chạy ra từ đó.

Ta có tổng cộng bao nhiêu phương trình như thế này? Đếm thì thấy tổng cộng là V phương trình, nhưng thực ra chúng không độc lập với nhau. Có thể thấy điều này bằng cách lấy tổng tất cả các phương trình trên. Ta sẽ được đồng nhất thức 0 = 0, vì ở vế trái với mỗi IAB bao giờ cũng có IBA. Vế phải thì tất nhiên tổng là 1 + (–1) cộng nhiều số 0, cũng bằng không. Như vậy chỉ có V – 1 phương trình độc lập.

Nhưng những phương trình trên không phải tất cả các phương trình ta phải viết ra. Có một loạt các phương trình khác (phương trình loại hai). Ta giả sử ABCD là một mặt (ta cho nó là tứ giác ở đây nhưng logic tiếp theo đúng với mọi đa giác). Ta sẽ có phương trình

IAB + IBC + ICD + IDA = 0.

Tại sao có phương trình này? Đó là do điện trở trên mỗi cạnh là 1 Ω nên IAB cũng là hiệu điện thế giữa hai đỉnh A và B: IAB = UA – UB. Từ đó phương trình ở trên trở thành hiển nhiên. Tổng cộng có F phương trình như vậy. Tuy nhiên các phương trình này cũng không độc lập, nếu cộng tất cả các phương trình này lại ta lại có đồng nhất thức 0 = 0, do đó là chỉ có F – 1 phương trình loại hai.

Tổng cộng ta có như vậy là (V – 1) + (F – 1) = V + F – 2 phương trình.

Ta phải giải các phương trình này để tìm các dòng IAB. Có bao nhiêu ẩn số tất cả? Số ẩn là số cạnh E.

Thiên nhiên cho ta biết khi nối mạch điện thì chỉ có một nghiệm duy nhất, vậy số phương trình phải bằng số ẩn.

Do đó V + F – 2 = E.

Đây chính là công thức Euler phải chứng minh.