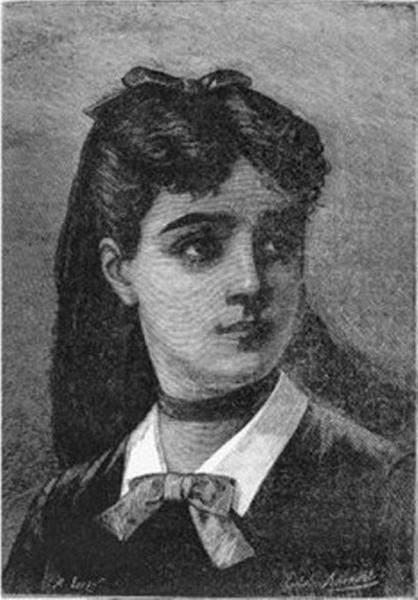Khoa Sư phạm

Tạp chí danh tiếng Smithsonian (Mỹ) từng bình chọn 5 nhà Toán học nữ nổi tiếng trong lịch sử. Những người phụ nữ này đã chứng minh rằng không có sự khác biệt giới tính trong lĩnh vực nghiên cứu Toán học - vốn được quan niệm chỉ dành cho nam. Trong lĩnh vực nghiên cứu này nhiều khi phụ nữ cũng có thể hoàn thành xuất sắc hơn họ

1. Hypatia (370 - 415) người Ai Cập

Hypatia thành Alexandria được coi là người phụ nữ đầu tiên có đóng góp đáng kể cho sự phát triển của Toán học. Bà là người phụ nữ tài năng và xinh đẹp, một người thầy tôn kính trong lòng học trò. Cuộc đời của bà như một bản anh hùng ca, vượt ra ngoài lĩnh vực học thuật, trở thành nguồn cảm hứng của nhiều tác phẩm văn học và nghệ thuật.

Nhà toán học nữ Hypatia.

Hypatia là con gái của nhà toán học Theon, giáo sư của Đại học Alexandria, người đã tự dạy bà về toán học, thiên văn học, và triết học. Ông từ chối áp đặt cho con gái mình vai trò truyền thống được giao cho phụ nữ thời đó và chăm sóc, nuôi dạy bà lớn lên như nuôi một người con trai theo truyền thống Hy Lạp. Nhà sử học Slatkin từng viết: "Phụ nữ Hy Lạp thuộc mọi tầng lớp đều bị cai quản và chủ yếu phải chăm lo đến các công việc trong gia đình như nội trợ, chăm sóc trẻ nhỏ... Nhưng Hypatia lại sống cuộc đời của một học giả được kính trọng tại đại học Alexandria ở một vị trí chỉ có nam giới mới được hưởng vào thời kỳ này”. Bà chưa bao giờ lập gia đình và sống độc thân suốt cuộc đời mình, cống hiến cho việc học và giảng dạy. Các nhà văn cổ đại đồng ý rằng bà là một người phụ nữ có trí thức sâu rộng, là điển hình của một phụ nữ mạnh mẽ, thông minh và kiên cường cho dù bà sống ở bất kỳ thời đại nào.

Mối quan tâm rộng lớn, ấn tượng nhất của Hypatia thuộc về toán học và thiên văn học. Bà đã viết và thuyết giảng về thiên văn học bao gồm các khía cạnh quan sát và về toán học như hình học và đại số, đồng thời thực hiện một tiến bộ trong kỹ thuật tính toán. Các bài viết của bà được đánh giá cao trong các lĩnh vực kỹ thuật của toán học. Sau khi cha bà qua đời, Hypatia đã tiếp tục chương trình do cha bà khởi xướng, đó là nỗ lực để bảo vệ và mở rộng các tác phẩm toán học vĩ đại trong di sản của đại học Alexandria. Thư viện lớn của Alexandria có tới 500.000 cuốn sách, là giáo sư tại trường đại học, Hypatia thỏa sức nghiên cứu các tài nguyên đồ sộ này và bà đã tận dụng hết khả năng của nó.

Mối quan tâm rộng lớn, ấn tượng nhất của Hypatia thuộc về toán học và thiên văn học.

Nhưng trong thời điểm xã hội tăm tối, tôn giáo đang được đề cao, những gì quá nổi trội và quá khác lạ đều có nguy cơ bị quy là dị giáo. Hypatia không những thuộc phe thân cận với chính quyền ngoại đạo Orestes và bị Cyril, Tổng giám mục của thành Alexandria coi là một "chướng ngại" đối với giáo hội, mà những khái niệm toán học và triết học của bà lại khá mâu thuẫn với giáo lý của nhà thờ. Đại học Alexandria là trung tâm của văn hoá và khoa học, nơi này cũng không hề ủng hộ các học thuyết của tôn giáo. Chính vì điều này Alexandria đã bị phá hủy và Hypatia đã trở thành biểu tượng của bi kịch, đến mức cái chết của bà đã trở thành hiện thân cho tất cả những gì đã mất của nền văn minh bị nhấn chìm trong sự hỗn loạn bởi mẫu thuẫn giữa khoa học và tôn giáo.

Vào năm 415, khi đang trên đường về nhà sau khóa giảng bài hàng ngày ở trường đại học, Hypatia bị tấn công bởi đám đông các giáo sĩ Cơ đốc, họ kéo xe của bà vào nhà thờ, và tại đây, bà đã bị sỉ nhục và bị đánh đến chết. Sau cái chết của Hypatia, Đại học Alexandria cũng bị thiêu cháy theo lệnh của Cyril, và những ngôi đền của những người ngoại giáo cũng bị phá hủy. Đã có một cuộc di cư tập thể của các nhà trí thức và các nghệ sĩ từ thành phố Alexandria di tản đến các nơi khác hòng cứu lấy tính mạng. Cyril sau đó được tôn thành một vị thánh vì những nỗ lực của ông ta trong việc trấn áp nền ngoại giáo và chiến đấu vì đức tin chân chính. Cái chết của Hypatia từ lâu đã được công nhận như là một dấu hiệu đầu nguồn trong lịch sử mô tả thời đại cổ điển của chủ nghĩa ngoại giáo từ thời Kitô giáo.

Cái chết của Hypatia trở thành một trong những vụ giết người có tính toán và tàn ác nhất trong lịch sử.

Cái chết của Hypatia trở thành một trong những vụ giết người có tính toán và tàn ác nhất trong lịch sử. Mặc dù bà mất đi nhưng tên tuổi của bà trường tồn trong lịch sử khoa học. Cuộc khủng hoảng chính trị và tôn giáo của thời đại ấy đã dẫn đến cái chết của bà những cũng đã khiến bà trở nên bất tử.

2. Sophie Germain (1776 - 1831), người Pháp

phie Germain là nhà nữ toán học nổi tiếng của Pháp. (Ảnh: Smithsonian).

Marie-Sophie Germain là một nhà toán học người Pháp tự học, người đã làm việc trên nhiều con đường phá vỡ các lý thuyết toán học vào cuối thế kỷ 18 và đầu thế kỷ 19. Germain không thể đến trường do cuộc Cách mạng Pháp nổ ra khi cô còn là một đứa trẻ nhưng cô không để điều đó ngăn cản việc học và cô tự dạy mình những nguyên tắc cơ bản của toán học với sự giúp đỡ của những cuốn sách trong thư viện của cha cô. Sophie Germain làm việc trên lý thuyết số và độ co giãn trong nhiều năm; cô ấy cũng đã nghiên cứu bằng chứng về Định lý cuối cùng của Fermat trong nhiều năm trước khi cuối cùng cô ấy có thể chứng minh điều đó cho đến cuối sự nghiệp. Cô thấy khó khăn khi được chấp nhận là phụ nữ trong một lĩnh vực mà sau đó bị đàn ông thống trị và trên thực tế, sự tham gia của phụ nữ không được khuyến khích; tuy nhiên điều đó không ngăn cô theo đuổi mục tiêu của mình. Sophie Germain đã trao đổi với một số nhà toán học hàng đầu thời bấy giờ bằng cách sử dụng bút danh và tiếp tục với công việc của mình để thể hiện loại tỷ lệ cược mà cô phải chiến đấu để có được sự nghiệp là một nhà toán học độc lập.

Tuổi thơ & cuộc sống sớm

Marie-Sophie Germain được sinh ra ở Paris, Pháp vào ngày 1 tháng 4 năm 1776 tại Ambrose-Francois Germain và Marie-Madeline Germain. Có một số tranh chấp liên quan đến nghề nghiệp chính xác của cha cô, nhưng theo hầu hết các tài khoản, anh ta hoặc là một thương gia thịnh vượng, buôn bán lụa hoặc thợ kim hoàn. Cô có hai chị em gái; một già và một trẻ

Sophie Germain chỉ mới 13 tuổi khi Cách mạng Pháp diễn ra và đó là lý do khiến cô phải ở trong nhà do bầu không khí rất dễ cháy ở Paris. Tuy nhiên, cô đã tự dạy mình những nguyên tắc cơ bản của toán học bằng cách đọc qua một vài cuốn sách về chủ đề được lưu giữ tại thư viện riêng của cha cha.

Năm 1794, Germain quyết định tận dụng chương trình giảng dạy toán học tại Ecole Polytechnique mới khai trương. Mặc dù theo quy định, phụ nữ bị cấm ở Polytechniqu, cô được phép nắm giữ các bài giảng. Joseph-Louis Legrange, một nhà toán học tại viện đã trở thành cố vấn của cô. Cô đã sử dụng bút danh nam M. LeBlanc trong thư từ của mình để mọi người không thể hiểu rằng cô là phụ nữ.

Nghề nghiệp

Năm 1798, Sophie Germain bắt đầu quan tâm đến lý thuyết số sau khi đi qua cuốn sách ‘Theorie des Nombres, được xuất bản bởi nhà toán học Adrien-Marie Legendre. Germain đã gửi cho cô một số ý tưởng của riêng mình về chủ đề lý thuyết số và độ co giãn, mà nhà toán học đã xuất bản như là bổ sung của phiên bản thứ hai của cuốn sách gốc của mình.

Sau khi đọc cuốn sách Carl Friedrich Gauss, ‘Disquisitiones Arithmeticae, Sophie Germain đã viết cho tác giả vào năm 1804 về những ý tưởng của riêng mình liên quan đến Định lý cuối cùng của Fermat. Theo nhiều người, các lý thuyết của Germain đã không có bằng chứng chắc chắn và cô không bao giờ nhận được phản hồi từ Gauss về chủ đề này.

Viện Hàn lâm Khoa học Pháp đã tiến hành một cuộc thi toán học, trong đó các thí sinh phải đưa ra một lời giải thích toán học liên quan đến các thí nghiệm được thực hiện bởi nhà khoa học Ernst F.F. Chladini trên đĩa rung. Germain nộp tác phẩm của mình vào năm 1811, hai năm sau khi giải thưởng được công bố nhưng bài báo của cô đã bị từ chối. Nhà toán học Adrien-Marie Legendre tuyên bố rằng lý thuyết Germain không phải là một phổ quát.

Sophie Germain tiếp tục phấn đấu cho giải thưởng toán học do Viện hàn lâm Khoa học Pháp cung cấp và sau khi liên tục thất bại trong việc gây ấn tượng với ban giám khảo; cuối cùng cô đã giành được giải thưởng vào năm 1816 trên tờ giấy xử lý các rung động trên bề mặt cong và mặt phẳng. Cô là người phụ nữ đầu tiên được trao giải thưởng đó.

Trong suốt phần sau của sự nghiệp, Sophie Germain đã làm việc với Định lý cuối cùng của Fermat và hợp tác với Legendre, cuối cùng cô đã có được nó vào năm 1825. Đó là công việc vĩ đại nhất trong sự nghiệp của Germain. Cô cũng nghiên cứu một chút về triết học cũng như tâm lý học sau này trong cuộc sống.

Sophie Germain được chẩn đoán mắc bệnh ung thư vú vào năm 1829 nhưng điều đó không ngăn cản cô tiếp tục thực hiện các lý thuyết của mình và hai năm sau khi được chẩn đoán; bài viết của cô về độ cong của các bề mặt đàn hồi đã được công bố trên tạp chí khoa học danh tiếng.

Công trình chính

Sophie Germain là một trong những nhà toán học quan trọng nhất trong thời đại của cô. Cô ấy đã làm công việc tiên phong trong lĩnh vực của mình trong lý thuyết số và công việc quan trọng nhất của cô là chứng minh Định lý cuối cùng của Fermat.

Giải thưởng & Thành tích

Sophie Germain sống trong thời đại mà phụ nữ weren khuyến khích tiếp tục theo đuổi khoa học và do đó, mặc dù cô đã đạt được rất nhiều trong cuộc đời của mình như là một nhà toán học; cô đã không được trao giải thưởng nào. Tuy nhiên, cô đã trở thành người phụ nữ đầu tiên giành giải thưởng toán học do Viện hàn lâm giải thưởng Pháp trao tặng nhưng đó không phải là một giải thưởng mà là một giải thưởng mà cô giành được khi tham gia một cuộc thi

3. Ada Lovelace (1815 - 1852), người Anh

Hơn một thế kỷ trước khi con người thực sự tạo ra được một chiếc máy tính, Ada Lovelace đã tưởng tượng ra chiếc máy tính hiện đại. Chiếc máy đó có thể được lập trình để làm theo các hướng dẫn để phục vụ cho nhiều mục đích, không chỉ có thể tính toán mà còn có thể tạo ra nhiều thứ khác, vì nó “dệt ra các mô hình đại số giống như cách cái máy dệt Jacquard dệt ra hoa và lá”.

Ada Lovelace được coi là nhà lập trình đầu tiên trên thế giới. Nguồn: aptechvietnam.com.vn

Theo Live Science, Ada Lovelace được biết tới bởi những đóng góp đối với máy tính vạn năng thời đầu của Charles Babbage, The Analytical Engine - máy phân tích. Trong những ghi chép của bà liên quan tới máy phân tích có bao gồm cả thuật toán (algorithm) đầu tiên được viết với mục đích để máy tính xử lý. Vì điều này, bà thường được coi là nhà lập trình đầu tiên trên thế giới.

Gia thế và cuộc đời của Nữ toán học tài năng Ada Lovelace

Augusta Ada King, nữ bá tước Lovelace (10/12/1815 - 27/11/1852), tên khai sinh là Augusta Ada Byron, và thường được biết tới với tên gọi Ada Lovelace. Bà là người con hợp pháp duy nhất của nhà thơ lãng mạn Anh George Gordon Byron (hay còn gọi là Nam tước Byron vừa nổi tiếng về thơ ca, vừa khét tiếng trăng hoa) và bà Anne Isabella "Annabella" Milbanke. Nếu cha của bà nổi tiếng bởi trí tưởng tượng và tài năng về thơ ca thì mẹ của Ada - bà Annabella Byron lại là người đối lập hoàn toàn bởi niềm đam mê với các con số và toán học. Nam tước Byron đã từng gọi vợ mình là “công chúa của Hình bình hành”. Cha mẹ Ada ly thân khi cô còn nhỏ và cha cô qua đời khi cô chỉ mới lên 8. Ada lớn lên trong kỷ luật với định hướng giáo dục xoay quanh số học, âm nhạc và tiếng Pháp. Bà Byron muốn kiềm chế trí tưởng tượng của con gái mình vì cảm thấy đấy là một “mối đe dọa” đến từ gene nhà Byron.

Nhưng Ada Lovelace đã hòa giải hai thái cực của cả cha và mẹ. Với Ada, trí tưởng tượng là một “sự kết hợp”, nắm bắt điểm chung giữa những đối tượng tưởng như không có mối liên hệ rõ ràng. Trí tưởng tượng là ngành “khám phá”, là sự thâm nhập vào thế giới vô hình xung quanh - thế giới của Khoa học.

Bức họa Ada Lovelace năm 1836. Nguồn: britannica.com

Nhờ vào xuất thân quyền quý, cô được học với các gia sư riêng, các trí thức trong giới khoa học và văn học Anh. Ada ngẫu nhiên được bao quanh bởi những nhà tư tưởng lớn của thời đại ấy, bao gồm Mary Somerville – nhà khoa học kiêm nữ nhà văn nổi tiếng.

Somerville chính là người đã giới thiệu Ada với Charles Babbage khi cô 17 tuổi. Tại một cuộc họp do Charles Babbage tổ chức, ông đã cho Ada thấy một cái máy tính cơ học bằng đồng cao khoảng 60cm và nó đã nhanh chóng khuấy động trí tưởng tượng của cô gái trẻ. Họ nhanh chóng tìm thấy sự đồng điệu về toán học và khoa học để rồi sự hợp tác ấy đã mở đường cho một ngành khoa học mới: khoa học về máy tính hay ngành công nghệ thông tin. Cũng qua Somerville, Ada Lovelace gặp chồng tương lai của mình - William King. Họ kết hôn năm 1835, khi bà mới 19 tuổi. King nhanh chóng trở thành bá tước, và Ada trở thành nữ bá tước xứ Lovelace. Đến năm 1839, bà đã sinh hai con trai và một con gái.

Tuy nhiên, cuộc sống hôn nhân hay gia đình không hề gây ảnh hưởng đến quá trình học tập của Ada Lovelace. Trong bức thư bà viết cho Somerville sau khi kết hôn: “Bây giờ tôi đã đọc Toán mỗi ngày và chìm đắm trong lượng giác và đã học sơ bộ về phương trình bậc 3 và bậc 4”. Năm 1840, Ada Lovelace đề nghị Augustus De Morgan, một giáo sư toán học ở London, dạy kèm cho bà. Thông qua trao đổi thư từ, ông đã dạy toán học cao cấp ở trình độ đại học cho Ada. Ông đã từng viết thư cho mẹ Ada và nhận xét rằng: nếu một nam sinh thể hiện khả năng xuất sắc như Ada, chắc hẳn anh ta sẽ trở thành một nhà toán học xuất chúng.

Cuộc gặp gỡ định mệnh với Charles Babbage

Như đã đề cập bên trên, năm 17 tuổi, Ada gặp một người đàn ông khiến cuộc đời cô thay đổi: Charles Babbage. Babbage là một kỹ sư, một nhà thiên văn học và cũng là một nhà phát minh.

Charles Babbage - một kỹ sư, một nhà thiên văn học và cũng là một nhà phát minh người Anh. Nguồn: thinglink.com

Thiên văn học vào thời ấy đòi hỏi rất nhiều tính toán, và Babbage muốn tạo ra một chiếc máy một chiếc máy không bao giờ thấy buồn chán và cũng không bao giờ mắc lỗi để có thể làm những công việc hỗ trợ cho hoạt động nghiên cứu của ông.

Vào những năm 1820, khi chưa hề có chip máy tính, không bóng bán dẫn, thậm chí cũng chưa có điện, nhưng điều này không ảnh hưởng gì tới mong muốn của Babbage. Ông sử dụng các bánh răng, dây curoa và các thiết bị cơ khí khác để tạo ra chiếc máy và đặt tên cho nó là Máy khác thường. Babbage đã dành ra 20 năm và sử dụng một khoản tiền khổng lồ của chính phủ vào dự án này, nhưng công nghệ thời đó chưa đủ phát triển nên ông không bao giờ làm cho cỗ máy của mình hoạt động được.

Khi Ada gặp Charles, ông đã nói với cô ấy về ý tưởng mới của mình. Đó là một cái máy phức tạp hơn cả máy khác thường trước, ông gọi nó là máy phân tích, và nó có thể làm bất kỳ kiểu tính toán nào. Ada đã rất ngạc nhiên và thích thú với ý tưởng này, cô tìm cách giúp Babbage làm cho chiếc máy hoạt động. Trong những bức thư kéo dài từ năm 1835 đến năm 1852, Babbage nói về những kế hoạch của ông còn Ada Lovelace thì thể hiện những tham vọng của mình.

Tháng 9 năm 1842, Ada được yêu cầu dịch một bài báo mô tả về công cụ phân tích của Babbage được viết bởi nhà toán học, kỹ sư người Ý Luigi Federico Menabrea (sau này trở thành thủ tướng Italy) cho một tạp chí Thụy Sĩ.

Ada Lovelace không chỉ dịch bài báo sang tiếng Pháp, mà còn viết thêm những ghi chú của riêng mình, tiên đoán tiềm năng sử dụng to lớn của cỗ máy trong tương lai. Phiên bản của bà dài đến 20 ngàn chữ so với bản gốc chỉ có 8 ngàn chữ, hay theo như Babbage: “Những ghi chú của Nữ bá tước xứ Lovelace dài gấp ba lần chiều dài của bài viết ban đầu... Tác giả đã chạm đến gần như toàn bộ những câu hỏi khó khăn và trừu tượng nhất của vấn đề”.

Bản dịch của Lovelace được xuất bản năm 1843 và được coi là một cột mốc quan trọng trong ngành khoa học máy tính: Bà mô tả rất rõ ràng cách thiết bị của Babbage hoạt động và liên tưởng tới máy dệt Jacquard để giải thích nguyên lý của nó: cũng giống như máy dệt tự động Joseph-Marie Jacquard phát minh có thể tạo ra hình ảnh từ các thẻ đục lỗ, hệ thống của Babbage sẽ dùng các bánh răng để dệt nên phương trình đại số.

Một trong hai bức ảnh của bà Ada Lovelace, được chụp bởi Antoine Claudet vào thời gian bà đã tạo ra “Ghi chú” của mình về máy tính. Nguồn: elle.vn

Trong bản phụ chú, Ada Lovelace đã tìm ra một lỗi trong thuật toán cỗ máy dùng để tính chuỗi số Bernoulli (chuỗi số hữu tỷ thường được sử dụng trong toán học lý thuyết hay số học). Bà cũng giả thuyết một phương pháp cho công cụ lặp lại một loạt các hướng dẫn, một quá trình được gọi là vòng lặp mà các chương trình máy tính ngày nay thường sử dụng. Ada cũng đưa ra các khái niệm tư duy chuyển tiếp và đề xuất một thuật toán cho phép máy thực hiện các lệnh để nó phản ứng với các ứng dụng thực tế khác ngoài tính toán.

Chương trình tính số Bernoulli do Ada Lovelace viết (trong quyển sách Phác thảo về Công cụ tính toán của Luigi Menabrea, minh họa bằng những ghi chép của Ada Lovelace). Nguồn: tiasang.com.vn

Bản phụ chú phát triển bản mô tả của Menabrea sâu sắc đến mức mà sau đó được các chuyên gia coi là một công trình riêng của Ada Lovelace, và được đặt tên là "Những chú thích". Nội dung của nó thực sự là một chương trình cho máy tính. Trước đó, chưa ai làm ra một chương trình tương tự.

Bên cạnh đó, Ada Lovelace cũng tiên đoán sự ra đời của kỷ nguyên máy tính, đưa ra quan điểm rằng những máy móc tính toán phức tạp, hay gọi là máy tính (computer), cần phải có thêm những tính năng khác, xử lý được những ký hiệu logic khác, ngoài tính toán các con số đơn thuần.

Ada Lovelace thậm chí đề cập đến "công cụ có thể sáng tác một cách khoa học, tỉ mỉ công phu âm nhạc ở bất kỳ mức độ phức tạp và rộng mở nào".  Thời đó, ngay cả người thầy Charles Babbage của bà cũng chưa từng có một sự hình dung như vậy.

Ada Lovelace qua đời vào ngày 27 tháng 11 năm 1852 vì căn bệnh ung thư tử cung. Bà được chôn cất bên cạnh cha của mình, ở trong nghĩa địa của Nhà thờ Thánh Mary Magdalene ở Nottingham, Anh. Tác phẩm của bà, được tái khám phá vào giữa thế kỷ 20 và trở thành nguồn cảm hứng để Bộ Quốc phòng đặt tên cho một ngôn ngữ lập trình theo tên bà: ngôn ngữ lập trình Ada.

Nhiều năm về sau, các học giả vẫn tranh cãi có đúng Ada Lovelace đã viết những dòng ghi chú này? Nhưng với những tài liệu hiện có thì không thể phủ nhận những gì đóng góp của bà Ada Lovelace là tiền đề quan trọng cho sự ra đời của ngành tin học hiện đại ngày nay, đặc biệt là thế giới lập trình.

Bắt đầu từ năm 2009, người ta lấy ngày Thứ Ba thứ hai của tháng 10 làm ngày Ada Lovelace – ngày tôn vinh những thành tựu của phụ nữ trong lĩnh vực “khoa học, công nghệ, kỹ thuật và toán học” (STEM).

4. Sofia Kovalevskaya (1850 - 1891), người Nga

Khởi phát đam mê toán học từ thưở bé

Sofia Kovalevskaya có điều kiện phát triển trí thông minh toán học là nhờ sự đầu tư giáo dục tốt hơn hẳn các cô bé cùng trang lứa và được thừa hưởng gen di truyền từ gia đình. Mẹ cô là một phụ nữ xinh đẹp, thông minh và nói được 4 ngôn ngữ châu Âu. Cha cô cũng là một người thông minh, được giáo dục tốt và quan tâm tới việc giáo dục các con nên đã thuê cho các con mình những gia sư tốt nhất để vượt qua trở ngại trong môn toán.

Ngoài ra, Sofia còn có điều kiện phát huy trí tưởng tượng rộng mở của trẻ thơ khi cả gia đình cô đến ở hẳn tại Palibino ở Tây Bắc nước Nga năm cô lên 8. Đó là một ngôi nhà lớn ở giữa “một khu vực thưa dân và hoang dã” với quang cảnh thiên nhiên hùng vĩ: phía bên này là rừng xanh, phía bên kia là các đồng cỏ, đồi cao và hồ nước đẹp tuyệt vời trải dài hàng kilomet. Trước đó, công việc đại tướng pháo binh của cha khiến cho gia đình cô phải di chuyển thường xuyên.

Niềm đam mê toán học của Sofia bắt đầu từ những cuộc trò chuyện thuở ấu thơ với người chú ham đọc sách và thường chia sẻ nhiều kiến thức, ý tưởng với cô cháu gái, chú Pyotr Vasilievich Korvin-Krukovsky. Trong trí óc non nớt của cô bé Sofia, chú Pyotr có “sự kính trọng sâu sắc” với toán học. Chính những bài nói chuyện của chú Pyotr về các khái niệm toán học đã cuốn hút mạnh mẽ tâm trí Sofia vào một “thế giới mới của những điều kỳ diệu mà những người bình thường không thể tiếp cận”, theo những gì bà viết trong nhật ký.

Ngay lúc đó, Sofia không thể hiểu được các khái niệm này nhưng cô càng học toán thì năng khiếu toán của cô càng trỗi dậy. Cô đã áp dụng những cách thức tương tự các nhà toán học để hiểu được các công thức lượng giác trong một cuốn sách vật lý của nhà vật lý ở gần nhà cô. Kỹ thuật của cô đã khiến tác giả cuốn sách ấn tượng đến nỗi ông đã ra sức thuyết phục cha của Sofia gửi cô đến các lớp học tư ở St. Petersburg, một trong các trung tâm nghiên cứu toán học hàng đầu châu Âu thời điểm đó.

Triết lý của Sofia Kovalevskaya những năm giữa tuổi hai mươi đầy nhiệt huyết, đam mê toán học và say mê sáng tác văn học. Ảnh: Novosti Press Agency.

Kết hôn giả để được du học về toán

Đến tuổi trưởng thành, vì là phụ nữ Sofia không được học đại học ở Nga. Để thỏa mãn khát khao tri thức, năm 1868 Sofia dàn dựng việc kết hôn với một nhà tự nhiên học trẻ tuổi và chuyển đến Heidelberg (Đức) năm 1869. Cô đã xin phép từng giáo sư để được tham gia một số bài giảng về vật lý và toán học. Chẳng bao lâu sau các giáo sư nhận ra sự thông tuệ về toán học của cô, mọi người trong trường đại học nhỏ ở thành phố Heidelberg đều xôn xao về “một cô gái người Nga gây kinh ngạc”.

Sự nổi tiếng vẫn không thay đổi khát khao học tập mạnh mẽ của Sofia. Năm 1870, Sofia chuyển đến Berlin và làm việc với giáo sư Karl Weierstass, một trong các giáo sư toán học hàng đầu châu Âu và thế giới thời đó. Berlin là trung tâm nghiên cứu toán học quan trọng nhất ở Đức lúc bất giờ. Sau khi kiểm tra khả năng của bà, ông đã nhận bà vào các lớp học riêng (bà bị đại học Berlin từ chối vì là nữ). Dưới sự hướng dẫn của ông, Sofia đã viết ra 3 công trình xuất sắc: chuyển động của sao Thổ, tích phân elip, phương trình vi phân bán phần. Trong số này, phương trình vi phân bán phần là nghiên cứu chính thức giúp Kovalevkaia được công nhận tốt nghiệp tiến sĩ đại học Göttingen không qua các kỳ thi và học phần bắt buộc vào năm 1874 (với sự hỗ trợ của Karl Weierstrass). Đây cũng chính là công trình khoa học lớn đầu tiên giúp bà giành được sự công nhận rộng rãi của giới toán học thời đó.

Hi sinh hạnh phúc riêng để toàn tâm toàn ý cho toán học 

Sau khi tốt nghiệp tiến sĩ ở Đức, Sofia Kovalevskaya quay về Nga nhưng vẫn không được giới khoa học Nga nhìn nhận vì sự phân biệt giới tính. Bà tạm dừng việc nghiên cứu để dành nhiều thời gian cho gia đình, niềm đam mê viết văn rồi sinh một con gái năm 1878. Năm 1881, vì một số lý do bà quyết định ly thân với chồng trong 2 năm.

Năm 1883, chồng bà Vladimir Kovalevkaya đã tự vẫn trong tuyệt vọng vì phá sản và bị tố lừa đảo chứng khoán, Trước biến cố này, Sofia đã gửi con lại cho chị gái, đồng ý lời mời sang Thụy Điển làm giảng viên toán học đại học Stockholm từ Magnus Mittag-Leffler, nhà toán học Thụy Điển sáng lập tạp chí toán quốc tế Acta Mathematica và có nhiều đóng góp quan trọng trong sự tiến bộ của trường phái toán học Scandinavi.

Tuy nhiên, đây chỉ là một vị trí không lương tạm thời. Đến năm sau (1884) Sofia mới được ký hợp đồng có lương 5 năm với đại học Stockholm và được mời tham gia ban biên tập Acta Mathematica, một trong các tạp chí toán quốc tế thuộc loại lâu đời và danh giá nhất thế giới, trở thành người phụ nữ đầu tiên làm biên tập viên một tạp chí khoa học. Bà cũng là người phụ nữ đầu tiên được phong viện sĩ thông tấn của viện hàn lâm khoa học Saint Petersburg trong cùng năm.

Năm 1888, bà công bố nghiên cứu về “sự quay của vật thể rắn quanh một điểm cố định”. Công trình này sau đó đã được trao giải Prix Bordin của Viện Hàn lâm Khoa học Pháp, giải thường vào loại danh giá nhất của các viện hàn lâm.

Một năm sau, năm 1889, công trình trên nhận thêm một giải khác từ Viện Hàn lâm Khoa học Thụy Điển và bản thân Sofia được thăng chức thành giáo sư trọn đời của trường đại học Stockholm.

Thật không may là khi đang ở đỉnh cao sự nghiệp, Sofia Kovalevskaya mắc bệnh viêm phổi và qua đời vào năm 1891, lúc chỉ mới bước qua tuổi 40.

Thành tựu về khoa học 

Tổng kết lại sự nghiệp khoa học, Sofia Kovalevskaya là nhà toán học nữ lớn đầu tiên ở Nga. Vượt lên sự kỳ thị giới tính và thiệt thòi của nữ giới khi theo đuổi khoa học, Sofia Kovalevskaya đã có nhiều đóng góp quan trọng cho toán học thế giới về tích phân, phương trình vi phân bán phần và cơ khí. Tổng cộng bà đã xuất bản 10 nghiên cứu về toán học và vật lý toán học, trong đó có nhiều công trình lớn được ứng dụng trong toán học và khoa học hiện đại, theo Famous Women.

 

Trong công trình đạt giải của viện Hàn lâm Khoa học Pháp “sự quay của vật thể rắn quanh một điểm cố định”, bà đã khám phá cái mà ngày nay được gọi là “Đỉnh Kovalevskaya”, là trường hợp khác duy nhất của chuyển động vật rắn hoàn toàn có thể tích phân được ngoài các đỉnh Euler và Lagrange.

Với những gì đã làm được, Sofia Kovalevskaya được giới toán học phương Tây chấp nhận mình là một thành viên “ngang hàng với các nhà toán học nam” trong thời đại của mình, theo một nhà viết tiểu sử hiện đại, dù các nghiên cứu của bà chưa có được một công trình nào thật sự mang tính mở đường hay tạo ra một trường phái mới trong toán học.

Hình tượng Sofia Kovalevskaya hi sinh hạnh phúc gia đình, phấn đấu không mệt mỏi cho sự nghiệp đã trở thành nguồn cảm hứng lớn lao cho phong trào nữ quyền ở châu Âu và cổ vũ cho nhiều chị em nữ giới theo chân bà vào đại học trong thời của bà. Bà hoàn toàn xứng đáng với danh hiệu nữ hoàng toán học, có mặt trong mọi cuộc bình chọn những nhà toán học nữ tài năng nhất trong lịch sử nhân loại.

5. Emmy Noether (1882 - 1935), người Đức

Tên đầy đủ của người phụ nữ ấy là Amalie Emmy Noether. Bà sinh năm 1882 trong một gia đình gốc Do Thái tại thành phố Erlangen, Bavaria, Đức. Cha của bà, Max Noether, là GS Toán (tự học) tại ĐH Erlangen. Ông chuyên về lý thuyết hàm đại số, một ngành Toán mới tại châu Âu², sau này phát triển thành Hình-Đại số. Mẹ bà, bà Ida Amalia Kaufmann, thuộc gia đình khá giả ở Cologne.

Thời ấy, con gái không được vào các trường gymnasium, một loại trường Trung học tốt dành cho con trai, chuẩn bị cho học sinh vào ĐH sau khi tốt nghiệp. Nên Emmy ghi danh vào học trường Städtischen Höheren Töchterschule, một loại trường Trung học dành cho con gái. Bà tỏ ra có năng khiếu ngoại ngữ (Anh văn và Pháp văn). Sau Trung học, bà theo học trường sư phạm để được đào tạo thành cô giáo dạy ngoại ngữ trong những trường nữ. Năm 1900, vừa 18 tuổi, bà tốt nghiệp. Chưa bắt đầu vào nghề dạy học, bà đã thay đổi ý định. Thời ấy, các trường ĐH ở Đức không nhận nữ sinh. Bà xin phép đặc cách ghi tên vào ĐH Erlangen với tư cách dự thính để học Toán. Năm 1903, bà qua được kỳ thi tuyển để được vào ĐH danh tiếng Göttingen học dự thính một học kỳ. Ở đó bà được sự khuyến khích của một số GS Toán nổi tiếng như Hermann Minkowski, Felix Klein, và nhất là David Hilbert. Năm 1904, bà trở về Erlangen hoàn tất chương trình ĐH.

Emmy Noether (1882 – 1935).

Năm 1904, bà được GS Paul Gordan, người được mệnh danh là “vua của lý thuyết bất biến” nhận làm GS cố vấn (advisor). Nhờ vậy sau này lý thuyết bất biến đã giúp bà có nhiều khám phá quan trọng trong lĩnh vực Vật lý lý thuyết. Năm 1907, Emmy Noether 25 tuổi, tốt nghiệp Tiến sĩ loại xuất sắc (summa cum laude).

Năm 1908, TS Noether được tuyển làm giảng viên không lương tại trường ĐH Erlangen (qui chế này áp dụng cho mọi Tiến sĩ mới được tuyển). Mặc dù cha bà có trợ giúp tiền bạc, nhưng cuộc sống của bà khá chật vật.

Noether không ngừng nghiên cứu những công trình của Hilbert về Đại số và Lý thuyết số. Hilbert đã ảnh hưởng sâu đậm trên sự nghiệp của bà, và nhờ đó bà trở thành nhà Toán học đi tiên phong trong lĩnh vực Đại số trừu tượng sau này. Còn Hilbert thì ông biết khả năng của bà, ngay từ năm 1903 khi bà còn ngồi dự thính lớp của ông ở Göttingen, ông tận tình khuyến khích và giúp đỡ.

Năm 1905, thế giới Khoa học bị choáng váng khi một người thư ký 26 tuổi phụ trách bằng sáng chế ở thành phố Bern, Thụy Sĩ, tên là Albert Einstein, chứng minh được rằng không gian và thời gian quyện vào nhau để trở thành một cái gọi tên là không-thời-gian (space-time). Các nhà Toán học Klein, Hilbert và Minkowski cũng giật mình khi nghe nói rằng thời gian bị chậm lại đối với vật thể di chuyển quá nhanh và rằng vận tốc ánh sáng là điều duy nhất “bất biến” trong lý thuyết của Einstein, Thuyết tương đối đặc biệt (the special theory of relativity), vừa mới được công bố.

Sự cần thiết những công cụ Toán học mới cho Vật lý trở nên cấp thiết sau 10 năm thuyết tương đối đặc biệt ra đời. Năm 1915, Einstein lại làm cho thế giới bị choáng váng thêm một lần nữa khi ông trình bày Thuyết tương đối tổng quát (thegeneral theory of relativity), thuyết này bao gồm cả vấn đề lực hấp dẫn (gravity) và như vậy làm thay đổi sự hiểu biết của chúng ta về công trình của Newton, đưa chúng ta ra khỏi thế giới của Newton để đi tới thế giới cực biên của tốc độ và lực hấp dẫn vũ trụ, ở đó cơ học Newton không hoạt động được nữa. Ngay cả từ khi hoàn tất thuyết tương đối đặc biệt vào năm 1905, Einstein vẫn tiếp tục làm việc nhiều để áp dụng nguyên lý tương đối vào lý thuyết về lực hấp dẫn của Newton. Vào năm 1907, ông cố gắng tiếp cận thêm nữa nhưng không được, ông nhận ra rằng cần phải có thêm công cụ Toán mới.

Năm 1915, Einstein đến khoa Toán, ĐH Göttingen nói chuyện về những gì ông đang nghiên cứu trên các phương trình ten-xơ cho thuyết tương đối tổng quát, trong đó các phần tử là những mảng (arrays) các biến số. David Hilbert có mặt trong thành phần thính giả. Ông ghi chép rất cẩn thận những gì Einstein viết trên bảng. Rồi ông về phòng và làm một việc có lẽ ông không thích chút nào: từ công trình của Einstein ông cố tìm ra phương trình đúng của thuyết tương đối tổng quát. Khi ông nghĩ là ông đã tìm ra được nó rồi, ông liền gửi kết quả - phương trình ten-xơ 14 chiều (tức là 14 hàng biến số) - cho một tạp chí để công bố.

Trong cùng thời gian ấy, Einstein cũng đang tìm phương trình cho thuyết tương đối tổng quát của mình và ông đã có một cú đột phá: Ông đã tìm ra phương trình ten-xơ 10 chiều (tức là 10 hàng biến số) và gửi nó cho một tạp chí khác. Nhưng kết quả, phương trình của nhà Toán học sai, trong khi phương trình của nhà Vật lý đúng! Thì ra phương trình rườm rà 14 chiều của Hilbert thiếu tính chất quan trọng: tính bất biến.

Rõ ràng là Hilbert cần một ai đó hiểu được tính bất biến hơn ông để có thể hiểu Toán học trong thuyết tương đối tổng quát của Einstein. Khi ấy Hilbert và Klein bỗng nhớ lại người phụ nữ trẻ rất đặc biệt ngồi trong lớp của họ cách đây chừng mười năm, bây giờ người ấy đã công bố nhiều bài báo sâu sắc mà không mang tên một trường ĐH nào cả.

David Hilbert (1862 - 1943), người có ảnh hưởng rất lớn đến Emmy Noether.

Trước năm 1915, Noether đã là một nhà Toán học nổi tiếng theo cách riêng của mình rồi. Các bài báo của bà được đọc và quan tâm trên khắp thế giới. Nội dung của chúng chú trọng tới Đại số.

Năm 1915, Felix Klein, trưởng Khoa Toán và Hilbert mời bà về ĐH Göttingen làm giảng viên nhưng lại gặp phải sự chống đối dữ dội từ phía các GS Ngữ văn và Lịch sử³ và cuối cùng trường chấp nhận cho bà làm phụ tá không lương cho GS David Hilbert. Bà vẫn còn phải nhận sự giúp đỡ tài chính của cha bà.

Chẳng bao lâu sau khi tới Göttingen, bà chứng tỏ khả năng của bà và không phụ lòng tin của hai nhà Toán học Felix Klein và Hilbert: Bà trình bày với Khoa Toán hai định lý (nay mang tên Định lý Noether). Chúng cho thấy sự liên kết cao độ giữa khái niệm đối xứng trong Toán học và định luật rất quan trọng về sự bảo toàn trong Vật lý. Một cách chi tiết hơn, hai định lý này cho thấy khi biểu thức Lagrange (biểu thức do Lagrange phát minh liên quan đến vị trí vật lý của những yếu tố) thụ hưởng một loại đối xứng nào đó – nghĩa là khi nó bất biến dưới tác dụng của nhóm Lie, chẳng hạn như nhóm các phép quay của một vòng tròn – thì hệ thống vật lý qui định bởi biểu thức Lagrange ấy sẽ gây ra định luật bảo toàn. Như thế, các định lý Noether giải thích sự bảo toàn năng lượng, bảo toàn momentum và bảo toàn điện tích bằng ngôn ngữ của lý thuyết nhóm.

Thế chiến Thứ nhất chấm dứt, xã hội Đức có nhiều thay đổi. Với những thành quả xuất sắc của mình, Emmy Noether được chính thức công nhận là giảng viên (lecturer) tại ĐH Göttingen năm 1919 (năm bà 37 tuổi), nhưng vẫn làm việc không lương. Ba năm sau, năm bà 40 tuổi, bà mới nhận được lương chính thức!

Đầu năm 1920, bà quay trở lại ngành Đại số. Trong 4 năm qua, bà đã để nhiều thời gian và công sức chuyên tâm vào các vấn đề Toán học do Vật lý lý thuyết đòi hỏi.

Mùa Đông năm 1928-1929, bà được mời làm GS thỉnh giảng tại ĐH Moscow. Mùa Hè năm 1930, bà về thỉnh giảng tại ĐH Frankfurt.

Tại Đại hội các nhà Toán học Thế giới 1928 tổ chức tại Bologna, bà được vinh dự chọn làm một trong những diễn giả chính. Bốn năm sau, năm 1932, Đại hội các nhà Toán học Thế giới tổ chức tại Zürich cũng chọn bà đọc bài diễn văn chính thức.

Thời gian cuối đời của Noether

Adolf Hitler lên nắm chính quyền vào tháng 1 năm 1933. Thanh niên Quốc Xã hoạt động ở khắp mọi nơi trên nước Đức, ngay cả trong trường học. Tại trường ĐH Göttingen, ngay những ngày tháng đầu, người ta đã thấy biểu ngữ cổ xúy tệ phân biệt chủng tộc quá khích (bài Do Thái) treo trong sân tường, chẳng hạn như: “Sinh viên Aryan muốn học Khoa học từ người Aryan, không phải từ người Do Thái.”

Tiếp theo, Bộ Giáo dục, Khoa học và Nghệ thuật ban hành một đạo luật theo đó tất cả các giáo viên, giảng viên và GS người Do Thái hoặc có họ hàng với người Do Thái phải rời khỏi nhiệm sở.

Trong vòng vài tháng sau đó, nhiều nhà Toán học và nhà Khoa học rời khỏi Göttingen, trong số đó có Richard Courant⁴, Edmund Landau⁵, Emmy Noether, Paul Bernays⁶, Max Born⁷, Hermann Weyl và nhiều người khác. Một số thì tìm đường qua Mỹ, Thụy Sĩ, hoặc các nước phương Tây khác, còn một số còn lưu lại Đức nhưng không còn công việc gì nữa. Hào quang ở Göttingen kéo dài hơn một thế kỷ, nay đã tắt.

Tháng 4 năm 1933, Emmy Noether được trường ĐH Bryn Mawer, Pennsylvania, Mỹ, mời về, dưới sự bảo trợ của quỹ Rockefeller Foundation. Mùa Thu năm ấy, bà bắt đầu giảng dạy Toán cho sinh viên Cao học. Năm 1934, bà về Viện Nghiên cứu Cao cấp Princeton theo lời mời của nhà Toán học Oswald Veblen (1880 – 1960), nhà Hình học hàng đầu thế giới, đang phụ trách tại đó.

Mùa Hè năm 1934, bà trở về Đức thăm quê hương lần cuối. Tháng 4 năm 1935, bác sĩ chẩn đoán bà bị ung thư xương và qua đời sau khi phẫu thuật thất bại. Năm ấy bà 53 tuổi.

Ngày đưa tiễn bà chỉ có đồng nghiệp, những người cộng tác, và học trò của bà. Bà không lập gia đình, và ở Mỹ bà cũng không có bà con gần nào cả. Ngày đầu có Hermann Weyl, Richard Brauer và đông đảo GS của trường ĐH Bryn Mawer. Mấy ngày sau có Albert Einstein, van de Waerden, Pavel Alexandrov, và nhiều nhà Khoa học có tiếng khác từ nhiều nơi xa cũng kịp về chào bà lần cuối. Trong một buổi lễ tưởng nhớ bà Albert Einstein đã phát biểu: “Trong số những nhà Toán học nổi tiếng mà tôi biết hoặc tôi cùng làm việc thì Fräulein⁸ Noether là thiên tài có đầu óc sáng tạo nhất, cách xa so với bất cứ người phụ nữ có trình độ cao nào. Trong lĩnh vực Đại số, ngành hội tụ nhiều bộ óc xuất chúng trong nhiều thế kỷ, bà đã khám phá ra những phương pháp vô cùng quan trọng, giúp ích rất nhiều cho nhà Toán học thế hệ sau.”

Một số công trình của Noether:

- Năm 1920, 1921 bà cùng Werner Schmeidler công bố một bài báo về Lý thuyết về Ideals trong đó bà định nghĩa ideals trái, ideals phải từ một vành và bài về Dây chuyền tăng, Dây chuyền giảm của ideals (Ascending and descending chain conditions). Từ đây, có tên vành Noether. Nhà Đại số học Irving Kaplansky gọi công trình này là một cuộc cách mạng trong Đại số trừu tượng.

- Năm 1924, bà hợp tác cùng Bartel Leendert van der Waerden. Sau này 1931, van Waerden viết cuốn Moderne Algebra dựa trên những ghi chép khi làm việc với bà, cuốn sách là khuôn vàng thước ngọc cho giới học và dạy Đại số trong nhiều chục năm sau.

- Năm 1926, bà công bố bài báo Chứng minh Tính Hữu hạn của các Bất biến trong các Nhóm Tuyến tính với Đặc số p (Proof of the Finiteness of the Invariants of Finite Linear Groups of Characteristic p). Từ bài báo này, sau này chúng ta có Bổ đề chuẩn hóa Noether (Noether Normalization Lemma).

Chú thích:

 (1) Hermann Weyl (1885 – 1955), nhà Toán học Mỹ gốc Đức, một trong những người sáng lập ra Viện Nghiên Cứu Cao Cấp Princeton (IAS).

 (2) Vào thập niên 1960, ngành này được nhà Toán học xuất sắc và độc đáo Grothendieck làm mới và phát triển thêm lên.

 (3) Khi ấy Đức đang chủ động trong Thế chiến thứ I. Một GS Lịch sử nói: “Nghĩ thế nào khi những người lính của chúng ta trở về lại giảng đường ngồi dưới chân một người đàn bà nghe bà ấy giảng bài?” Hilbert trả lời: “Chúng ta đang ở trong một trường ĐH, không phải trong một nhà tắm.” Kimberling, Clark (1981), Emmy Noether and Her Influence.

(4) Richard Courant (1888 - 1972), nhà Toán học Mỹ gốc Đức, đã từng giảng dạy tại Göttingen, cứu về Toán ứng dụng và mặt tối thiểu.

(5) Edmund Landau (1877 - 1938), nhà Toán học Đức, giảng dạy tại Göttingen, chuyên về Lý thuyết số và Giải tích phức.

(6) Paul Bernays (1888 – 1977), nhà Toán học Đức gốc Thụy sĩ, chuyên về Logic Toán.

(7) Max Born (1882 - 1970), nhà Toán học và vật lý lý thuyết Đức, giảng dạy tại Göttingen, chuyên về Cơ học lượng tử.

(8) Cô Noether, nói một cách kính trọng.