Khoa Sư phạm

Tóm tắt

GeoGebra là phần mềm toán học đặc biệt được sử dụng miễn phí trên thế giới và có cả giao diện tiếng Việt. Nó kết hợp giữa môi trường hình học động, đại số động và tính toán động. Trong đó, giáo viên có thể dựng các hình vẽ hình học hay làm việc với các hàm số, đồng thời thao tác được với các biểu thức tọa độ của nó. Hơn thế nữa GeoGebra còn có khu vực nhập thông tin các đối tượng trực tiếp. Bài viết trình bày về việc khai thác phần mềm GeoGebra hỗ trợ cho hoạt động dạy học giải bài tập Hình học không gian lớp 11.

Từ khóa: phần mềm GeoGebra, hình học không gian, hoạt động giải bài tập Toán.

1. Đặt vấn đề

Chúng ta biết rằng Hình học không gian là phần kiến thức khó và trừu tượng trong chương trình môn Toán Trung học phổ thông, để học tốt môn này đòi hỏi học sinh (HS) phải có tư duy trực quan, tư duy tính toán, tư duy logic và sự tưởng tượng cao. Vì lẽ đó, nhiều HS ngại học Hình học không gian hay kết quả của môn học này chưa được tốt. Trong dạy học Hình học không gian, có những hoạt động dạy học nếu chỉ sử dụng các phương tiện truyền thống, giáo viên (GV) khó có thể giúp HS hiểu và hình dung được một số tri thức trừu tượng, khám phá các tính chất, định lí toán học, giải bài tập,…

Phần mềm GeoGebra là phần mềm có nhiều thế mạnh: dễ sử dụng, dễ dàng chuyển đổi được ngôn ngữ sử dụng. Một mặt có thể được sử dụng để nhận dạng khái niệm toán học cũng như để tạo ra các tài liệu giảng dạy. Mặt khác, GeoGebra có tính năng để thúc đẩy học tập tích cực và lấy HS làm trung tâm bằng cách cho phép thực hiện các thực nghiệm toán học, khám phá tương tác, cũng như khám phá trong học tập Toán, góp phần giúp việc dạy học toán trở nên thuận lợi và hiệu quả hơn. Vì vậy, có thể hỗ trợ GV khắc phục những hạn chế, khó khăn khi sử dụng các phương tiện dạy học truyền thống; góp phần tạo động cơ, hứng thú học tập cho HS, mang lại sự tương tác cao giữa HS và GV trong giờ dạy, giúp HS học tập hiệu quả hơn.

Nghiên cứu về việc sử dụng phần mềm GeoGebra trong dạy học môn Toán ở trường phổ thông là một vấn đề mang tính thời sự và có tính ứng dụng thực tiễn cao đã và đang thu hút nhiều nhà khoa học quan tâm, nghiên cứu. Gần đây, cũng đã có một số công trình trong và ngoài nước nghiên cứu về vấn đề này: Cách sử dụng phần mềm Geogebra trong dạy học khám phá chương “phép dời hình và phép đồng dạng” lớp 11 Trung học phổ thông [1]; Sử dụng GeoGebra để củng cố lí thuyết hình học [3]; Khả năng thông thạo công nghệ trong giải quyết vấn đề Toán học của học sinh với phần mềm GeoGebra [5]…

Từ những lý do trên cho thấy GeoGebra là phần mềm dạy học Toán đáng được quan tâm nghiên cứu và đưa vào sử dụng rộng rãi, nhằm góp phần ứng dụng mạnh mẽ công nghệ thông tin vào giảng dạy Toán ở trường phổ thông, nâng cao chất lượng dạy học. Vì vậy, chúng tôi chọn phần mềm GeoGebra cho nghiên cứu của mình. Bài viết đề cập đến việc khai thác phần mềm GeoGebra hỗ trợ cho hoạt động dạy học giải bài tập Hình học không gian lớp 11.

2. Nội dung nghiên cứu

2.1. Giới thiệu về phần mềm GeoGebra

“GeoGebra là phần mềm toán học động được thiết kế cho việc dạy và học Toán học từ tiểu học đến đại học. Phần mềm là sự kết hợp giữa môi trường hình học động, thao tác tính toán với các biểu thức đại số, giải tích và bảng tính điện tử trong mặt phẳng tọa độ. Vì vậy, nó cho phép thu hẹp khoảng cách giữa các lĩnh vực toán học của hình học, đại số, giải tích và thậm chí cả tính toán.

Tác giả phần mềm là Markus Hohenwarter, giảng viên Trường Đại học Salzburg, Cộng hòa Áo. Phần mềm GeoGebra được khởi tạo năm 2001 và liên tục được phát triển.

GeoGebra là phần mềm chạy dựa trên nền Java và nó có thể chạy trên mọi hệ điều hành. Người dùng chỉ cần vào trang web: https://www.geogebra.org/ để tải và cài đặt phần mềm vào máy tính là có thể sử dụng được. Với các phiên bản mới GeoGebra có thể xuất bản với giao diện web, nhúng vào phần mềm Powerpoint và có thể xử lí các thao tác như trên phần mềm GeoGebra tạo cho người dùng thuận lợi hơn rất nhiều khi trình chiếu hay trong giảng dạy.

Geogebra là phần mềm miễn phí, mã nguồn mở, đa ngôn ngữ (trong đó có tiếng Việt). Giao diện của GeoGebra thân thiện và dễ sử dụng, với các hộp công cụ trực quan người dùng có thể thao tác với phần mềm một cách dễ dàng. Khi ta dùng trỏ chuột vào một công cụ nào đó thì sẽ xuất hiện hướng dẫn để dùng công cụ tương ứng đó, điều này hỗ trợ nhiều cho những người dùng chưa nắm rõ cách dùng nút lệnh. Nếu không thích sử dụng chuột và các nút lệnh thì người dùng có thể thao tác với phần mềm qua hệ thống nhập các câu lệnh, GeoGebra giúp người dùng sử dụng dễ dàng hơn khi cung cấp một hệ thống hỗ trợ gợi ý và hướng dẫn nhập các câu lệnh. GeoGebra với nhiều tính năng mạnh mẽ, dễ sử dụng, có sự kết hợp của hệ thống máy tính đại số, các phần mềm hình học tương tác và các bảng tính, giúp người dùng có thể tiết kiệm được thời gian và không gian lưu trữ trên máy tính. Đặc biệt, người dùng có thể tạo thêm công cụ mới theo nhu cầu của họ. Ngoài ra GeoGebra còn có tính cộng đồng lớn với kho dữ liệu tài nguyên phong phú do người dùng khắp nơi chia sẻ để tham khảo, thực hiện các ý tưởng toán học” [4].

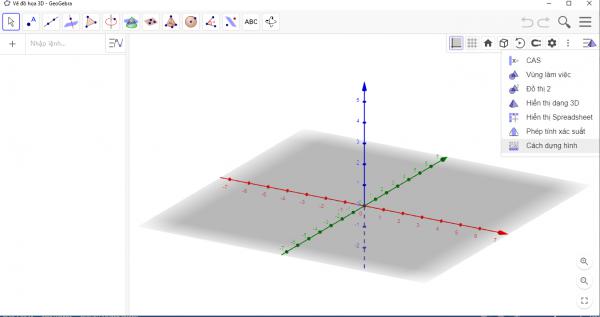
Hình 1. Giao diện vẽ hình không gian của phần mềm GeoGebra

2.2. Dạy học hoạt động giải bài tập Hình học không gian lớp 11 với sự hỗ trợ của phần mềm GeoGebra

Theo tác giả Nguyễn Bá Kim: Ở thời điểm cụ thể nào đó, mỗi bài tập chứa đựng tường minh hay ẩn tàng những chức năng khác nhau (chức năng dạy học, chức năng giáo dục, chức năng phát triển, chức năng kiểm tra). Những chức năng này định hướng tới việc thực hiện các mục đích dạy học. Thông qua giải bài tập, HS thực hiện các hoạt động (HĐ) như nhận dạng và thể hiện định nghĩa, định lý, quy tắc, phương pháp, những hoạt động toán học phức hợp, những hoạt động trí tuệ phổ biến trong toán học. Yêu cầu của lời giải là: Không có sai lầm, phải có căn cứ chính xác, phải đầy đủ. Ngoài ra, trong dạy học giải bài tập còn yêu cầu lời giải ngắn gọn, đơn giản nhất, cách trình bày rõ ràng và hợp lý [2].

Hình học không gian lớp 11 luôn là một chủ đề khó đối với GV và HS để hình thành các khái niệm, chứng minh định lý và tìm phương pháp giải bài tập. Làm thế nào để HS học tập chủ đề này một cách tích cực, chủ động, sáng tạo, không những hiểu được đầy đủ bản chất khái niệm mà còn biết vận dụng một cách linh hoạt để giải toán luôn là hướng nghiên cứu, tìm tòi với nhiều GV. Dạy học giải bài tập về Hình học không gian lớp 11 với sự hỗ trợ của phần mềm Geogebra có thể được tiến hành theo các bước sau:

- Bước 1: Tìm hiểu nội dung bài toán

Sử dụng phần mềm GeoGebra vẽ hình để tìm hiểu bài toán, xác định các yếu tố ban đầu, nêu rõ giả thiết, kết luận của bài toán. Dùng công thức, kí hiệu, phát biểu đề bài dưới những dạng khác nhau.

- Bước 2: Xây dựng chương trình giải bài toán

Dựa vào yêu cầu bài toán để xác định bài toán đó thuộc dạng toán nào? Sử dụng phần mềm cho thay đổi hình vẽ để quan sát các yếu tố cần tìm hiểu để từ đó phát hiện ra những vị trí đặc biệt, những mối quan hệ, tính chất bất biến của các đối tượng trong bài toán, lựa chọn phương hướng giải và giải theo hướng đã chọn.

 - Bước 3: Thực hiện chương trình giải bài toán

Soạn thảo lời giải của bài toán.

 - Bước 4: Đánh giá và nghiên cứu sâu lời giải bài toán

Sau khi giải xong, chúng ta sử dụng các chức năng của các phần mềm để minh họa, kiểm tra lại kết quả và toàn bộ quá trình giải toán và cho thay đổi các yếu tố đầu bài của bài toán để từ đó có thể:

+ Khái quát hóa rút ra tri thức phương pháp để giải một bài toán, một dạng toán cụ thể nào đó;

+ Xây dựng bài toán tương tự, mở rộng bài toán;

+ Thực hiện thao tác đặc biệt hóa để khai thác các kết quả có thể có của bài toán;

+ Sử dụng kết quả bài toán này để giải một số bài toán đã gặp.

Ví dụ 1. Cho tứ diện ABCD. Trên AD lấy điểm E. Gọi  là mặt phẳng qua E song song với AC và BD. Thiết diện của tứ diện cắt bởi là hình gì?

GV có thể tổ chức hoạt động nhận thức cho HS với phần mềm GeoGebra như sau:

Bước 1: Tìm hiểu nội dung bài toán

Khi tiếp nhận bài toán này GV yêu cầu HS xác định:

+ Giải thiết của bài toán: Cho tứ diện ABCD, ;  qua M và .

+ Kết luận: Thiết diện của tứ diện cắt bởi là hình gì?

+ Nhận dạng bài toán: Xác định thiết diện của chóp cắt bởi .

Bước 2: Xây dựng chương trình giải bài toán

Hoạt động 1. HS vẽ hình

Để trợ giúp HS trong HĐ này thì GV hướng dẫn HS sử dụng GeoGebra dựng hình theo thiết kế kịch bản như thể hiện ở của sổ dựng hình.

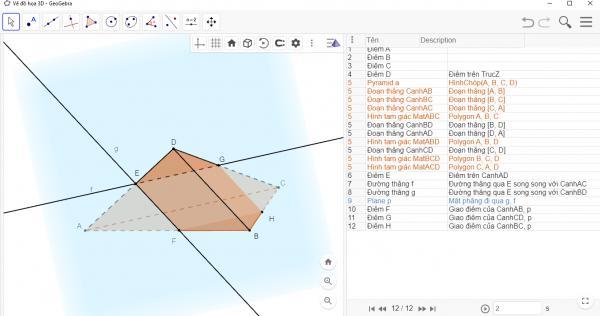
Hình 2. Hình vẽ thể hiện kịch bản dựng hình cho ví dụ 1

GV: Mặt phẳng (a) đi qua M và song song với AC, BD thì sẽ cắt (ADC), (ABD) theo giao tuyến như thế nào?

HS: Giao tuyến là đường thẳng f và g đi qua M và lần lượt song song với AC, BD.

1. Mặt phẳng là mặt phẳng được xác định như thế nào?

HS: (a) đi qua f và g.

HĐ 2. HS dựa vào hình vẽ dự đoán hình dạng của thiết diện.

1. Thao tác để có thể quan sát hình ở nhiều góc độ.
2. Dùng lệnh di chuyển hình vẽ và quan sát hình vẽ với các hướng khác nhau.

GV: có dự đoán gì về hình dạng của thiết diện thu được ở hình vẽ.

HS: Thiết diện là hình bình hành.

GV: Hãy lập luận xét tương tự cho các mặt còn lại của hình chóp.

HS: g cắt AB tại F, thì giao tuyến của  với (ABC) đi qua F và song song với AC sẽ cắt BC tại H. Vậy . Giao tuyến f cắt AC tại G, giao tuyến của thì .

GV: Thiết diện là gì?

HS: Thiết diện là tứ giác EFHG.

GV: Giải thích tại sao thiết diện đã cho là hình bình hành như đã dự đoán từ hình vẽ?

HS: Thiết diện là hình bình hành vì có các cặp cạnh đối song song.

Bước 3: Thực hiện chương trình giải bài toán

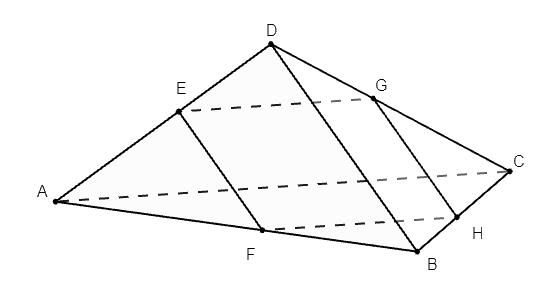
Hình 3. Hình vẽ minh họa cho ví dụ 1

 qua E và song với đường thẳng AC nên cắt các mặt phẳng (ACD), (ABC) lần lượt theo các giao tuyến .

 qua E và song với đường thẳng BD nên cắt các mặt phẳng (ABD), (BCD) lần lượt theo các giao tuyến .

Vậy, thiết diện là tứ giác EFHG .

Mặt khác  và  nên thiết diện là hình bình hành.

Bước 4: Đánh giá và nghiên cứu sâu lời giải bài toán

GV tổ chức nhận xét, chỉnh sửa bài làm của HS trên bảng.

GV: Từ cách giải bài toán này, hãy rút ra các bước giải dạng toán xác định thiết diện của hình chóp có giao tuyến song song với đường thẳng.

HS rút ra quy trình giải:

+ Xác định giao tuyến của với mặt phẳng chứa đường thẳng song song với  (hay còn gọi là xác định giao tuyến gốc).

+ Xác định giao điểm của  với các cạnh của chóp.

+ Xác định giao tuyến của  với các mặt của hình chóp.

+ Kết luận thiết diện.

GV yêu cầu HS giải bài tập tương tự:

Bài tập 1: Cho tứ diện ABCD. Gọi E là điểm nằm trong tam giác ABC. Mặt phẳng (P) qua E và song song với AC, BD. Xác định thiết diện của ABCD với (P). Thiết diện là hình gì? Tại sao?

Bài tập 2: Cho hình chóp S.ABCD có đáy ABCD là một tứ giác lồi. Gọi O là giao điểm của hai đường chéo AC và BD. Xác định thiết diện của hình chóp cắt bởi  đi qua O, song song với AB và SC. Thiết diện là hình gì? Tại sao?

Ví dụ 2. Cho hình chóp S.ABCD có AB không song song với CD, điểm E nằm trên cạnh SA. Gọi F là giao điểm của (EBC) với đường thẳng SD, G là giao điểm của BE và CF, H là giao điểm của BF và CE, I là giao điểm của AC và BD, J là giao điểm của AB và CD. Quỹ tích điểm G, H khi E di động trên cạnh SA lần lượt là:

1. Đường tròn đường kính SJ, SI.
2. Đường thẳng SJ, SI.
3. Đoạn thẳng SJ, SI.
4. Nửa đường tròn đường kính SJ, SI.

Đây là một câu hỏi trắc nghiệm nên GV có thể tổ chức hoạt động nhận thức cho HS với phần mềm GeoGebra như sau:

Hoạt động 1: HS vẽ hình dự đoán quỹ tích:

Trong bài tập này nếu HS chỉ vẽ một trường hợp của hình và phán đoán thì rất khó, hay suy luận ra quỹ tích cũng gặp khó khăn vì chỉ quan sát được hình ảnh bất động của đối tượng tại một vị trí. HS phải có khả năng tư duy, trí tưởng tượng và biết liên hệ giữa điểm chung của hai mặt phẳng với giao tuyến.

Để trợ giúp HS trong HĐ này thì GV hướng dẫn HS dựng hình bằng phần mềm GeoGebra bằng cách thiết kế kịch bản thể hiện ở của sổ dựng hình:

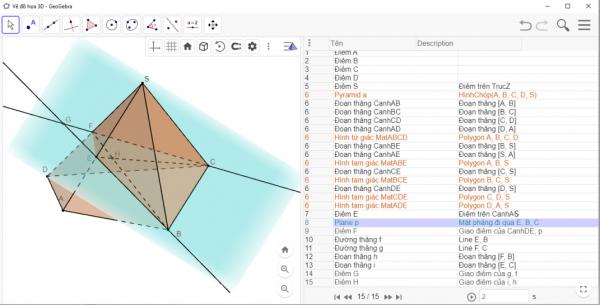
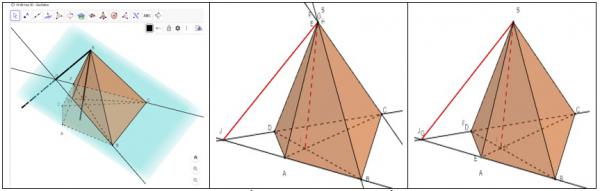
Hình 4. Hình vẽ thể hiện kịch bản dựng hình cho ví dụ 2

GV: Để dự đoán được quỹ tích cần thềm thao tác gì?

HS: Tạo vết cho điểm G và điểm H; Sau đó cho E di chuyển trên cạnh SA.

GV: Yêu cầu HS quan sát hình động và cho nhận xét.

HS: Quan sát trên màn hình thấy vết mà điểm G, H để lại có hình dạng là một đoạn thẳng.

GV: Có nhận xét gì về vị trí của G, H khi  và khi . Từ đó kết luận giới hạn của quỹ tích.

HS: Khi  thì .

Khi  thì ; ; .

HĐ 2. Đưa ra đáp án cho bài toán:

GV: Hãy chọn đáp án.

HS: Đáp án C là đáp án đúng.

Hình 5. Hình vẽ tạo vết của G, H khi E di chuyển trên cạnh SA

Hoạt động 3. Khai thác bài toán:

Từ hình vẽ dựng bằng phần mềm GeoGebra, GV gợi ý HS di chuyển các đỉnh của ABCD thay đổi so với giả thiết ban đầu của bài toán sao cho ABCD là hình thang đáy là AB và CD; hoặc ABCD là hình bình hành,... và theo dõi vết của G và H khi E di chuyển trên cạnh SA, từ đó gợi ý HS có thể sáng tạo ra bài toán mới bằng cách thay đổi giả thiết “AB không song song CD” bằng điều kiện “ABCD là hình thang đáy là AB và CD; hoặc ABCD là hình bình hành,...” để được bài tập mới.

Như vậy chúng ta thấy rằng với sự hỗ trợ của phần mềm GeoGebra, bài toán quỹ tích phức tạp sẽ được giải quyết một cách dễ dàng. Đặc biệt đối với các bài tập dạng trắc nghiệm thì việc sử dụng phần mềm để giải toán sẽ là một công cụ hữu hiệu giúp HS nhìn nhận nhanh và chính xác kết quả đồng thời phát triển năng lực đặc biệt hóa để sáng tạo ra bài tập mới.

3. Kết luận

Việc hướng dẫn giải bài tập Toán cho HS là một điều cần thiết và có vai trò quan trọng trong toàn bộ quá trình học tập của HS. GV biết cách sử dụng phần mềm dạy học mà cụ thể ở đây là phần mềm GeoGebra vào việc hỗ trợ giải toán liên quan đến Hình học không gian là rất phù hợp, nó góp phần rút ngắn thời gian vẽ hình, giúp đỡ trong dự đoán, giúp đỡ trong kiểm tra kết quả một cách dễ dàng nhằm đổi mới phương pháp dạy học, tăng hứng thú và hiệu quả học tập của HS ở các trường THPT là cần thiết. Để làm được điều này các trường phổ thông cần trang bị đầy đủ hơn nữa các phương tiện dạy học hiện đại như máy chiếu, màn hình, phòng học chức năng..., bổ sung các phần mềm dạy học có bản quyền vào thư viện nhà trường để các GV có thể chủ động sử dụng nó một cách hiệu quả nhất. Bản thân các GV phải tích cực hơn nữa trong tự học, tự nghiên cứu, ứng dụng các phần mềm vào hoạt động dạy học để các tiết dạy thêm sinh động, hiệu quả. Tích cực đẩy mạnh hơn nữa việc ứng dụng công nghệ thông tin, sử dụng phần mềm vào dạy học. Trong khuôn khổ bài báo, chúng tôi đã khai thác phần mềm GeoGebra để hỗ trợ dạy học hoạt động giải bài tập Hình học không gian ở lớp 11. Thông qua việc vận dụng phần mềm vào quy trình giải bài tập ở trên, tính hiệu quả của việc áp dụng phần mềm GeoGebra vào dạy hình không gian đã được thể hiện rõ ràng.

________________

Tài liệu tham khảo

[1] Nguyễn Văn Cảng (2015), Sử dụng phần mềm Geogebra trong dạy học khám phá chương “phép dời hình và phép đồng dạng” lớp 11 Trung học phổ thông, Luận văn thạc sĩ Sư phạm Toán, Đại học Quốc gia Hà Nội.

[2] Nguyễn Bá Kim (2015), Phương pháp dạy học môn Toán, NXB Đại học Sư phạm.

[3] Vũ Thị Phương (2021), Sử dụng GeoGebra để củng cố lí thuyết hình học, Tạp chí Khoa học Trường Đại học Sư phạm Thành phố Hồ Chí Minh, Tập 18 số 5, tr 817-826.

[4] Markus Hohenwarter, Judith Hohenwater, Yves Kreis, Zsolt Lavicza (2008), Teaching and calculus with free dynamic mathematics software GeoGebra (Dạy học và tính toán với phần mềm toán học động miễn phí GeoGebra), ICME 11, Mexico.

[5] Hélia Jacinto, Susana Carreira (2017), Mathematical Problem Solving with Technology: the Techno-Mathematical Fluency of a Student - with – GeoGebra (Giải quyết vấn đề toán học bằng công nghệ: Khả năng thông thạo công nghệ trong  giải quyết vấn đề Toán học của học sinh với GeoGebra), International Journal of Science and Mathematics Education, Springer, Vol. 15, issue 6.