Khoa Sư phạm
Trường Đại học Hà Tĩnh

Một triệu đô la dành cho ai giải được bất kỳ bí ẩn nào trong số bảy bí ẩn toán học. Đó chính là phần thưởng do một tổ chức tư nhân nêu ra nhằm đưa toán học trở lại vị trí xứng đáng của nó. Và dĩ nhiên, cũng để trả lời những câu hỏi lớn vẫn làm đau đầu các nhà toán học bấy lâu nay.
Hội đồng khoa học của Viện Clay (tập hợp những chuyên gia kiệt xuất trong tất cả các ngành toán học, và đầu tiên phải kể tên Andrew Wiles, người đã chứng minh “định lí cuối cùng của Fermat”) đã đánh liều tiếp nối con đường của Hilbert để nêu ra 7 bài toán cho thế kỉ 21. Giải thưởng Millennium Prize với trị giá 1 triệu USD/giải vô cùng hấp dẫn sẽ dành cho ai giải được bất kì bài nào trong số 7 bài toán thiên niên kỷ nổi tiếng do Viện toán học Clay đặt ra. Nó đã làm cho các nhà toán học phải đau đầu cho đến hiện nay.
- Giả thuyết Poincaré
Henri Poincare (1854-1912), là nhà vật lý học và toán học người Pháp,
một trong những nhà toán học lớn nhất thế kỷ 19. Giả thuyết Poincaré là một trong những giả thuyết toán học nổi tiếng và quan trọng bậc nhất do Jules-Henri Poincaré đưa ra năm 1904, và được Grigori Perelman chứng minh vào năm 2002, 2003. Trong 100 năm tồn tại, nó trực tiếp và gián tiếp đem về 4 huy chương Fields cho Smale (1966), Thurston (1982), Freedman (1986) và Perelman (2006).”
Nội dung giả thuyết: chứng minh là trong không gian 3 chiều, mọi bề mặt liên thông đơn giản hữu hạn và không có biên đều là bề mặt của một vật hình cầu.
Ví dụ chứng minh:
Lấy một quả bóng (hoặc một vật hình cầu), vẽ trên đó một đường cong khép kín không có điểm cắt nhau, sau đó cắt quả bóng theo đường vừa vẽ: bạn sẽ nhận được hai mảnh bóng vỡ. Làm lại như vậy với một cái phao (hay một vật hình xuyến): lần này bạn không được hai mảnh phao vỡ mà chỉ được có một.
Trong hình học topo, người ta gọi quả bóng đối lập với cái phao, là một về mặt liên thông đơn giản. Một điều rất dễ chứng minh là trong không gian 3 chiều, mọi bề mặt liên thông đơn giản hữu hạn và không có biên đều là bề mặt của một vật hình cầu.
Vào năm 1904, nhà toán học Pháp Henri Poincaré đặt ra câu hỏi: Liệu tính chất này của các vật hình cầu có còn đúng trong không gian bốn chiều. Điều kỳ lạ là các nhà hình học topo đã chứng minh được rằng điều này đúng trong những không gian lớn hơn hoặc bằng 5 chiều, nhưng chưa ai chứng minh được tính chất này vẫn đúng trong không gian bốn chiều.

Giả thuyết Poincaré do ông Jules-Henri Poincaré đưa ra (Nguồn: Internet)
- Vấn đề P chống lại NP
Với quyển từ điển trong tay, liệu bạn thấy tra nghĩa của từ “thằn lằn” dễ hơn, hay tìm một từ phổ thông để diễn tả “loài bò sát có bốn chân, da có vảy ánh kim, thường ở bờ bụi” dễ hơn? Câu trả lời hầu như chắc chắn là tra nghĩa thì dễ hơn tìm từ.
Những các nhà toán học lại không chắc chắn như thế. Nhà toán học Canada Stephen Cook là người đầu tiên, vào năm 1971, đặt ra câu hỏi này một cách “toán học”. Sử dụng ngôn ngữ logic của tin học, ông đã định nghĩa một cách chính xác tập hợp những vấn đề mà người ta thẩm tra kết quả dễ hơn (gọi là tập hợp P), và tập hợp những vấn đề mà người ta dễ tìm ra hơn (gọi là tập hợp NP). Liệu hai tập hợp này có trùng nhau không? Các nhà logic học khẳng định P khác NP. Như mọi người, họ tin rằng có những vấn đề rất khó tìm ra lời giải, nhưng lại dễ thẩm tra kết quả. Nó giống như việc tìm ra số chia của 13717421 là việc rất phức tạp, nhưng rất dễ kiểm tra rằng 258357 * 3843 = 13717421. Đó chính là nền tảng của phần lớn các loại mật mã: rất khó giải mã, nhưng lại dễ kiểm tra mã có đúng không. Tuy nhiên, cũng lại chưa có ai chứng minh được điều đó. “Nếu P = NP, mọi quan niệm của chúng ta đến nay là sai. Một mặt, điều này sẽ giải quyết được rất nhiều vấn đề Tin học ứng dụng trong công nghiệp; nhưng mặt khác lại sẽ phá hủy sự bảo mật của toàn bộ các giao dịch tài chính thực hiện qua Internet” - Stephen Cook thông báo.
Vấn đề P chống lại NP có vai trò rất quan trọng trong Khoa học máy tính và là tổng hòa của các vấn đề thuộc nhiều lĩnh vực: Toán học, Triết học, Sinh vật học và Mật mã.
- Các phương trình của Yang-Mills
Các nhà toán học luôn chậm chân hơn các nhà vật lý. Nếu như từ lâu, các nhà vật lý đã sử dụng các phương trình của Yang-Mills trong các máy gia tốc hạt trên toàn thế giới, thì các ông bạn toán học của họ vẫn không thể xác định chính xác số nghiệm của các phương trình này. Được xác lập vào những năm 50 bởi các nhà vật lý Mỹ Chen Nin Yang và Robert Mills, các phương trình này đã biểu diễn mối quan hệ mật thiết giữa vật lý về hạt cơ bản với hình học của các không gian sợi. Nó cũng cho thấy sự thống nhất của hình học với phần trung tâm của thể giới lượng tử, gồm tương tác tác yếu, mạnh và tương tác điện từ. Nhưng hiện nay, mới chỉ có các nhà vật lý sử dụng chúng…
- Giả thuyết Hodge
Euclide sẽ không thể hiểu được gì về hình học hiện đại. Trong thế kỷ XX, các đường thẳng và đường tròn đã bị thay thế bởi các khái niệm đại số, khái quát và hiệu quả hơn. Khoa học của các hình khối và không gian đang dần dần đi tới hình học của “tính đồng đẳng”. Chúng ta đã có những tiến bộ đáng kinh ngạc trong việc phân loại các thực thể toán học, nhưng việc mở rộng các khái niệm đã dẫn đến hậu quả là bản chất hình học dần dần biến mất trong toán học. Vào năm 1950, nhà toán học người Anh William Hodge cho rằng trong một số dạng không gian, các thành phần của tính đồng đẳng sẽ tìm lại bản chất hình học của chúng…
- Giả thuyết Riemann
2, 3, 5, 7, …, 1999, …, những số nguyên tố, tức những số chỉ có thể chia hết cho 1 và chính nó, giữ vai trò trung tâm trong số học. Dù sự phân chia các số này dường như không theo một quy tắc nào, nhưng nó liên kết chặt chẽ với một hàm số do thiên tài Thụy Sĩ Leonard Euler đưa ra vào thế kỷ XVIII. Đến năm 1850, Bernard Riemann đưa ra ý tưởng các giá trị không phù hợp với hàm số Euler được sắp xếp theo thứ tự. Giả thuyết của nhà toán học người Đức này chính là một trong 23 vấn đề mà Hilbert đã đưa ra cách đây 100 năm. Giả thuyết trên đã được rất nhiều nhà toán học lao vào giải quyết từ 150 năm nay. Họ đã kiểm tra tính đúng đắn của nó trong 1.500.000.000 giá trị đầu tiên, nhưng … vẫn không sao chứng minh được. “Đối với nhiều nhà toán học, đây là vấn đề quan trọng nhất của toán học cơ bản” – Enrico Bombieri, giáo sư trường Đại học Princeton, cho biết. Và theo David Hilbert, đây cũng là một vấn đề quan trọng đặt ra cho nhân loại. Bernhard Riemann (1826-1866) là nhà toán học Đức. Giả thuyết Riemann do ông đưa ra năm 1850 là một bài toán có vai trò cực kỳ quan trọng đến cả lý thuyết số lẫn toán học hiện đại.
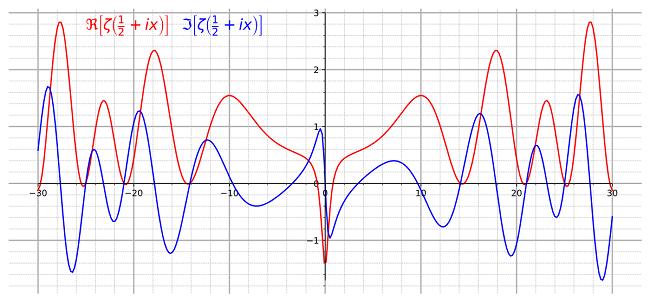
Giả thuyết Riemann (Nguồn: Internet)
- Các phương trình của Navier-Stokes
Chúng mô tả hình dạng của sóng, xoáy lốc không khí, chuyển động của khí quyển và cả hình thái của các thiên hà trong thời điểm nguyên thủy của vũ trụ. Chúng được Henri Navier và George Stokes đưa ra cách đây 150 năm. Chúng chỉ là sự áp dụng các định luật về chuyển động của Newton vào chất lỏng và chất khí. Tuy nhiên, những phương trình của Navier-Stokes đến nay vẫn là một điều bí ẩn của toán học: người ta vẫn chưa thể giải hay xác định chính xác số nghiệm của phương trình này. “Thậm chí người ta không thể biết là phương trình này có nghiệm hay không” – nhà toán học người Mỹ Charles Fefferman nhấn mạnh – “Điều đó cho thấy hiểu biết của chúng ta về các phương trình này còn hết sức ít ỏi”.
- Giả thuyết của Birch và Swinnerton-Dyer
Những số nguyên nào là nghiệm của phương trình x2 + y2 = z2 ? có những nghiệm hiển nhiên, như mathop 32 + 42 = 52 . Đây là phương trình vô số nghiệm, nó được chứng minh bởi Euclide cách đây 2300 năm.
Người ta cũng biết từ 30 năm nay rằng không có phương pháp chung nào cho phép tìm ra số các nghiệm nguyên của các phương trình dạng này. Tuy nhiên, đối với nhóm phương trình quan trọng nhất có đồ thị là các đường cong elip loại 1, các nhà toán học người Anh Bryan Birch và Peter Swinnerton-Dyer từ đầu những năm 60 đã đưa ra giả thuyết là số nghiệm của phương trình phụ thuộc vào một hàm số f: nếu hàm số f triệt tiêu tại giá trị bằng 1 (nghĩa là nếu f(1)= 0), phương trình có vô số nghiệm. nếu không, số nghiệm là hữu hạn
Giả thuyết nói như thế, các nhà toán học cũng nghĩ vậy, nhưng đến giờ chưa ai chứng minh được…
Người ta thấy vắng bóng ngành Giải tích hàm (Functional analysis) vốn được coi là lĩnh vực vương giả của nghiên cứu toán học. Lý do cũng đơn giản: những bài toán quan trọng nhất của Giải tích hàm vừa mới được giải quyết xong, và người ta đang đợi để tìm được những bài toán mới. Một nhận xét nữa : 7 bài toán đặt ra cho thế kỉ 21, mà không phải bài nào cũng phát sinh từ thế kỉ 20. Bài toán P-NP (do Stephen Cook nêu ra năm 1971) cố nhiên là bài toán mang dấu ấn thế kỉ 20 (lôgic và tin học), nhưng bài toán số 4 là giả thuyết Riemann đã đưa ra từ thế kỉ 19. Và là một trong 3 bài toán Hilbert chưa được giải đáp!
Một giai thoại vui: Vài ngày trước khi 7 bài toán 1 triệu đôla được công bố, nhà toán học Nhật Bản Matsumoto (sống và làm việc ở Paris) tuyên bố mình đã chứng minh được giả thuyết Riemann. Khổ một nỗi, đây là lần thứ 3 ông tuyên bố như vậy. Và cho đến hôm nay, vẫn chưa biết Matsumoto có phải là nhà toán học triệu phú đầu tiên của thế kỉ 21 hay chăng…
Trong số 7 bài toán này, mới chỉ có 1 bài được giải quyết. Đó là bài toán số 1 - Giả thuyết Poincaré. Người chiến thắng là nhà Toán học người Nga Grigori Perelman và sau khi phép chứng minh được thẩm định, Perelman đã được trao giải Fields năm 2006 và Millennium Prize 2010 (nhưng ông kiên quyết từ chối nhận giải).

Hội nghị sinh viên nghiên cứu khoa học năm học 2022- 2023 của Khoa Sư phạm đã thành công tốt đẹp trong niềm vui, sự tự hào của sinh viên và cán bộ giảng viên trong toàn Khoa.
Sáng ngày 19/4/2023, Hội nghị Sinh viên nghiên cứu khoa học - Khoa Sư phạm năm 2022 - 2023 được tổ chức tại Hội trường tầng 2, dãy nhà 15 tầng của Trường Đại học Hà Tĩnh. Tham dự Hội nghị có đại diện các khoa, phòng, ban, bộ môn trong nhà trường; toàn thể cán bộ, giảng viên, sinh viên của khoa và các giảng viên hướng dẫn.

Toàn cảnh Hội nghị
Hội nghị Sinh viên Nghiên cứu khoa học là hoạt động thường niên của Khoa, nhằm biểu dương những thành tích xuất sắc của sinh viên trong nghiên cứu khoa học. Hội nghị cũng chính là diễn đàn khoa học để sinh viên có cơ hội gặp gỡ, giao lưu, trao đổi kinh nghiệm trong hoạt động nghiên cứu khoa học; tạo điều kiện để các em công bố kết quả nghiên cứu, phát triển kỹ năng cần thiết góp phần xây dựng đội ngũ cán bộ, giáo viên trẻ có trình độ cao trong tương lai và nâng cao chất lượng đào tạo của Khoa nói riêng, của Nhà trường nói chung.

TS. Lê Văn An, Trưởng khoa phát biểu khai mạc hội nghị
Cũng như những năm học trước, Hội nghị Sinh viên nghiên cứu khoa học năm học 2022 – 2023 đã nhận được nhiều đề tài của sinh viên gửi tới dự thi. Trong số các đề tài đó, Hội đồng Khoa học của Khoa đã xét duyệt và lựạ chọn được 7 đề tài có chất lượng báo cáo tại Hội nghị.

ThS. Đặng Thị Yến, Phó Trưởng khoa Sư phạm, báo cáo tổng kết hoạt động NCKH năm học 2022 -2023
Năm nay, mặc dù số lượng đề tài không nhiều, nhưng lĩnh vực nghiên cứu khá phong phú, như: Toán cơ bản, Ứng dụng các phần mềm tin học trong dạy học toán, Phương pháp dạy học Toán ở tiểu học; Kĩ năng rèn luyện NVSP, Giáo dục và chăm sóc trẻ mầm non, Giáo dục môi trường cho HS tiểu học… và có những đề tài đề cập đến những nhu cầu thiết yếu của sinh viên như nhu cầu nhà trọ…

Một số đề tài NCKH được báo cáo
Nhìn chung, các bạn sinh viên đã biết lựa chọn những vấn đề có ý nghĩa thiết thực với nghề nghiệp cũng như những vấn đề thiết yếu của thực tiễn cuộc sống đặt ra để nghiên cứu. Phần lớn, các đề tài có cấu trúc logic, hợp lí, các nhiệm vụ đặt ra được giải quyết khá thấu đáo. Sau mỗi bài báo cáo, các tác giả đã nhận được nhiều ý kiến trao đổi, thảo luận hết sức sôi nổi, khách quan, khoa học từ Ban giám khảo, sinh viên và giảng viên tham gia Hội nghị.
Sau gần 4 tiếng đồng hồ làm việc một cách khách quan, công tâm, khoa học, Hội nghị Sinh viên nghiên cứu khoa học năm học 2022 – 2023 của khoa Sư phạm đã lựa chọn được những gương mặt tiêu biểu, xuất sắc trong hoạt động nghiên cứu khoa học của sinh viên, cụ thể: 1 giải nhất, 2 giải nhì, 2 giải ba và 2 giải khuyến khích.

Giải nhất “ Sinh viên NCKH” năm học 2022 - 2023 của nhóm tác giả Nguyễn Thị Trà Giang, Trần Thị Chi – Lớp K14 GDTH
Giải nhì “ Sinh viên NCKH” Năm học 2022 -2023 của nhóm tác giả Bùi Thị Hoàng Nhân, Phạm Thị Minh Hạnh – K12 GDTH; Nguyễn Thị Thuý Hằng, Trần Thị Hằng – K14 – GDTH
Giải ba “ Sinh viên NCKH” Năm học 2022 -2023 của tác giả Trần Thị Mỹ Thuận – K13 GDMN; Hoàng Thị Oanh K13 - GDTH
Giải khuyến khích “ Sinh viên NCKH” Năm học 2022 -2023 của tác giả Nguyễn Thị Hồng – K14 SP Toán; Hoàng Thị Oanh – Nguyễn Thị Thảo K13 - GDTH

Hội nghị Sinh viên Nghiên cứu khoa học năm học 2022 - 2023 của khoa Sư phạm đã khép lại nhưng sức lan tỏa, tầm ảnh hưởng của nó đến các bạn sinh viên vẫn còn đọng mãi. Ban tổ chức hi vọng rằng năm học 2023 – 2024 sẽ nhận được nhiều công trình nghiên cứu khoa học từ các bạn sinh viên gửi tới dự thi.

Khoa Sư phạm được thành lập theo Quyết định số 847/QĐ-TĐHHT, ngày 01/12/2017 của Hiệu trưởng trường Đại học Hà Tĩnh trên cơ sở sát nhập Khoa Sư phạm Tiểu học - Mầm non với Khoa Sư phạm Tự nhiên. Khoa hiện có 32 cán bộ giảng dạy và nghiên cứu, trong đó có 06 Tiến sỹ, 03 Nghiên cứu sinh, 22 Thạc sỹ, 04 cử nhân. Khoa Sư phạm đang đào tạo các ngành Sư phạm Toán học (7140209), Giáo dục Mầm non (7140201), Giáo dục Tiểu học (7140202), Sư phạm Vật lý (7140211), Sư phạm Hóa học (7140212).
Năm 2023, thực hiện đặt hàng của UBND tỉnh theo Nghị định 116, Khoa Sư phạm - Trường Đại học Hà Tĩnh tuyển sinh ngành Giáo dục Tiểu học, cụ thể:

- PHƯƠNG THỨC XÉT TUYỂN
Ngành Giáo dục Tiểu học tuyển sinh trong cả nước, xét tuyển dựa vào kết quả thi tốt nghiệp THPT Quốc Gia năm 2023; Học bạ THPT (năm lớp 11 hoặc lớp 12); xét tuyển thẳng theo quy định của Trường.
- TỔ HỢP XÉT TUYỂN
* C04 (Văn, Toán, Địa)
* D01 (Văn, Toán, Tiếng Anh)
* C14 (Ngữ văn, Toán, Giáo dục công dân)
* C20 (Ngữ văn, Địa lí, Giáo dục công dân)
- HỌC NGÀNH GIÁO DỤC TIỂU HỌC, bạn sẽ:
- Được miễn học phí!
- Được hỗ trợ chi phí học tập theo Nghị định 116!
- Được bố trí chỗ ở trong các ký túc xá tiện nghi!
- Được giới thiệu việc làm từ năm thứ 3!
- Có cơ hội nhận nhiều học bổng giá trị cao!
- HOÀN THÀNH CHƯƠNG TRÌNH ĐÀO TẠO, bạn sẽ:
-Vận dụng những nguyên lý cơ bản của chủ nghĩa Mác - Lênin; Đường lối cách mạng của Đảng Cộng sản Việt Nam; Tư tưởng Hồ Chí Minh; những chính sách của Đảng, chủ trương Nhà nước về phát triển kinh tế xã hội, giáo dục, văn hoá của đất nước vào quá trình dạy học tiểu học.
- Vận dụng kiến thức về Tâm lý học, Giáo dục học, Lý luận dạy học, Phương pháp dạy học bộ môn, Quản lý hành chính nhà nước và Quản lí ngành, có kiến thức phổ thông về môi trường, dân số, an ninh quốc phòng, an toàn giao thông, quyền trẻ em, y tế học đường để có thể thực hiện giáo dục tích hợp trong chương trình tiểu học.
- Có các kỹ năng mềm, khả năng tự học, có trình độ ngoại ngữ, ứng dụng công nghệ thông tin, biết vận dụng những hiểu biết về tình hình kinh tế - văn hoá – xã hội đời sống, phong tục tập quán của địa phương để có thể hoà nhập và góp phần phát triển cộng đồng.
- Phân tích được nội dung chương trình các môn học và các hoạt động giáo dục trong chương trình các lớp bậc Tiểu học.
- Cập nhật những thông tin đổi mới phương pháp giáo dục tiểu học trong nước và khu vực để khả năng vận dụng đổi mới phương pháp dạy học các môn học ở tiểu học.
- Lập kế hoạch giáo dục cho từng học kỳ và năm học, biết lập kế hoạch bài học theo định hướng đổi mới phương pháp dạy học, đổi mới phương pháp kiểm tra đánh giá ở tiểu học.
- Tổ chức các hoạt động dạy học phù hợp với điều kiện có thể của học sinh và địa phương nhằm phát huy tính tích cực, chủ động, sáng tạo của học sinh trong học tập. Biết dạy cho học sinh phương pháp học, đặc biệt là phương pháp tự học, phát triển ở học sinh năng lực tự đánh giá. Biết sử dụng các phương tiện công nghệ dạy học, đặc biệt là công nghệ thông tin vào quá trình dạy học ở tiểu học.
- Dạy lớp ghép, dạy tiếng Việt cho học sinh dân tộc, dạy học sinh khuyết tật, tàn tật theo hướng hòa nhập.
- Làm tốt công tác chủ nhiệm lớp, tổ chức các hoạt động giáo dục ngoài giờ lên lớp, hoạt động Sao nhi đồng, Đội thiếu niên tiền phong Hồ Chí Minh. Quản lý tốt lớp học, xây dựng lớp thành tập thể đoàn kết, tự quản; giáo dục học sinh cá biệt. Lập sổ sách, xây dựng và lưu trữ hồ sơ về quá trình học tập rèn luyện đạo đức của học sinh.
- Giao tiếp và ứng xử thích hợp với học sinh, gia đình học sinh, với đồng nghiệp và các tầng lớp nhân dân trong cộng đồng.
- THÔNG TIN LIÊN HỆ
Khoa Sư phạm, Trường Đại Học Hà Tĩnh.
- Tầng 6, nhà 15 tầng, Cẩm Bình, Cẩm Xuyên, Hà Tĩnh.
- Hotline: 0967.783.783
- Website: https://nse.htu.edu.vn/

Ngày 15/4/2023, Chi đoàn Cán bộ Khoa Sư phạm phối hợp với Chi đoàn Cán bộ Viện Toán học, Viện Hàn lâm Khoa học và Công nghệ Việt Nam tổ chức thành công chương trình “Hội thảo khoa học Các nhà nghiên cứu trẻ - Toán học và các ngành liên quan”.
Thực hiện kế hoạch năm học 2022-2023, nhận lời mời của chi đoàn Viện Toán học, Viện Hàn lâm Khoa học và Công Nghệ Việt Nam, tuổi trẻ khoa Sư phạm đã phối hợp tổ chức thành công Hội thảo khoa học các nhà nghiên cứu trẻ “Toán học và các ngành liên quan”. Đây là một trong các hoạt động nằm trong chuỗi sự kiện kỷ niệm 5 năm thành lập khoa Sư phạm. Hội thảo cũng là cơ hội để các nhà nghiên cứu trẻ của hai đơn vị chia sẻ kết quả nghiên cứu và tìm kiếm cơ hội hợp tác, phát triển. Hội thảo đã thu hút sự tham dự của đông đảo các giảng viên, nghiên cứu viên, học viên và sinh viên tới từ các đơn vị: Đại học Hà Tĩnh, Viện Toán học, Đại học Sư phạm Hà Nội, Đại học Thăng Long, Đại học Đà Nẵng, Đại học Giao thông vận tải, Học viện Tài chính. Hội thảo cũng vinh dự nhận được sự quan tâm và tham dự của TS. Đoàn Hoài Sơn (Bí thư đảng ủy, Hiệu trưởng Trường Đại học Hà Tĩnh), PGS.TSKH. Đoàn Thái Sơn (Quyền Viện trưởng Viện Toán học, Viện Hàn lâm Khoa học và Công nghệ Việt Nam), GS.TSKH. Đinh Nho Hào (Chủ tịch HĐKH Viện Toán học, Chủ tịch HĐKH Nafosted Ngành Toán, Tổng biên tập tạp chí Acta Mathematica Vietnamica), cùng các Phó giáo sư, Tiến sĩ là trưởng, phó phòng chuyên môn Viện Toán học, trưởng các đơn vị Trường Đại học Hà Tĩnh.

Phát biểu khai mạc, TS. Lê Văn An, Trưởng khoa Sư phạm, Trường Đại học Hà Tĩnh, Trưởng ban tổ chức Hội thảo, đã nhiệt liệt chào mừng các vị đại biểu, các nhà khoa học và các báo cáo viên về dự hội thảo. TS. Lê Văn An nhấn mạnh mối quan hệ hợp tác trong nghiên cứu - đào tạo giữa hai đơn vị và vai trò của nghiên cứu khoa học toán học đối với sự nghiệp đổi mới căn bản, toàn diện giáo dục Việt Nam. Về phía Viện Toán học, PGS.TSKH. Đoàn Thái Sơn đã thay mặt lãnh đạo Viện cám ơn Trường Đại học Hà Tĩnh, Khoa Sư phạm đồng ý phối hợp tổ chức hội thảo để cán bộ trẻ hai cơ quan có dịp giao lưu, chia sẻ và học hỏi lẫn nhau, cũng trong dịp này Chi đoàn Viện Toán học đã tặng Chi đoàn cán bộ giảng viên Khoa Sư phạm bộ sách Toán cao cấp do Viện Toán học chủ trì.

PGS.TSKH. Đoàn Thái Sơn, Q. Viện trưởng Viện Toán học phát biểu ý kiến

Chi đoàn Viện Toán tặng quà Khoa Sư phạm
Hội thảo diễn ra trong ngày 15/4/2023 với 10 báo cáo, trong đó có 8 báo cáo chuyên môn và 2 báo cáo giới thiệu về Khoa Sư phạm, Trường Đại học Hà Tĩnh và Viện Toán học được chia làm 3 phiên với các lĩnh vực chuyên môn Đại số, Giải tích, Hình học Tôpô, Xác suất thống kê và Quang học.


Thành công của Hội thảo “Toán học và các ngành liên quan - Hội thảo Khoa học các nhà nghiên cứu trẻ” sẽ thúc đẩy hoạt động nghiên cứu khoa học và hợp tác trong đội ngũ giảng viên, nghiên cứu viên trẻ của hai đơn vị. Đồng thời, gợi mở các hướng nghiên cứu mới, cơ hội học tập và tìm kiếm việc làm cho các học viên, sinh viên.
Một số hình ảnh trong Hội thảo




Mỗi một sinh viên chúng ta khi ngồi trên ghế giảng đường đại học đều luôn được nhà trường tạo điều kiện, cơ hội để tích lũy cho mình những kiến thức, kinh nghiệm cần thiết để làm hành trang bước vào nghề. Và những đợt thực tế, kiến tập, thực tập là cơ hội quý báu để sinh viên chúng tôi vận dụng những kiến thức mà thầy cô đã truyền thụ đưa vào thực tế để hoàn thiện bản thân và vững vàng bước vào nghề mình đã chọn sau này.

Bản thân tôi cũng như bao bạn sinh viên K12 và K27 khác, chúng tôi vừa bước qua kỳ thực tập tốt nghiệp kéo dài 2 tháng của mình. Khi bước qua kỳ thực tập đó, chắc hẳn sẽ có những bạn vui vì đạt được kết quả như mình mong muốn và cũng có bạn sẽ cảm thấy buồn vì chưa đạt được kết quả như mình mong đợi. Nhưng....chúng tôi đều mang trong mình một niềm tiếc nuối...giá như thời gian có thể trôi chậm lại để kỳ thực tập của mình diễn ra thật lâu hơn...
Nhớ lại những ngày đầu khi mới nhận được thông báo bản thân mình sẽ về thực tập ở Trường Mầm non Đại Nài, lúc đó trong tôi hiện lên cảm giác hồi hộp, lo lắng nhưng cũng đầy hứng thú và hy vọng. Tôi và các bạn trong đoàn đã tìm cho mình những người chị, người bạn từng thực tập ở ngôi trường này để tìm hiểu thêm về Ban giám hiệu, các cô ở đó. Cảm giác tò mò làm sao.
Rồi đến ngày ra mắt đoàn thực tập lại càng hiện lên trong bản thân tôi niềm khát khao muốn được thể hiện mình, niềm hy vọng lớn lao sẽ hoàn thành xuất sắc kỳ thực tập. Sau khi nghe báo cáo của trường, phát biểu của thầy hướng dẫn thì chúng tôi được nhà trường giới thiệu về cô chủ nhiệm và lớp mình sẽ thực tập. Bản thân tôi được phân vào lớp 5 tuổi B, có cô Nguyễn Thị Anh và cô Huỳnh Thị Minh Hòa làm chủ nhiệm. May mắn thay, năm nay thực tập tôi được đồng hành cùng bạn Hà Nhi - người bạn đã thực tập chung một lớp với tôi trong khoảng thời gian thực tập 1 của mình.

Sau khi kết thúc buổi ra mắt, đoàn thực tập chúng tôi được các cô chủ nhiệm dẫn về các lớp. Vừa đi vừa được nghe các cô trò chuyện, giới thiệu về lớp học mà mình sẽ thực tập, cảm giác hào hứng biết bao. Lớp 5 tuổi B mà tôi sẽ gắn bó 2 tháng tiếp theo là một lớp có tổng số 34 bạn, 20 bạn nam và 14 bạn nữ, lớp học có tổng số đông nhất trường. Bấy giờ trong đầu tôi hiện lên suy nghĩ vừa mừng, vừa lo: “ Khi gặp các bạn nhỏ không biết các bạn sẽ cảm thấy như thế nào? 2 tháng tiếp theo mình thực tập mình có làm tốt nhiệm vụ của mình không? Đây là lần đầu tiên được thực tập ở lớp 5 tuổi, không biết mọi thứ có khó quá không?...” Bao nhiêu câu hỏi hiện hữu trong đầu và chưa có câu trả lời thì lớp học mà tôi sẽ thực tập 2 tháng đã ở ngay trước mắt...Chúng tôi được cô chủ nhiệm giới thiệu sẽ về thực tập ở lớp 2 tháng cho các bạn nhỏ nghe. Các bạn đứng dậy lễ phép chào chúng tôi, cảm giác lúc đó thật hồi hộp.
Trong tuần đầu tiên thực tập chúng tôi được các cô chủ nhiệm hướng dẫn các phần việc cần làm trong quá trình thực tập và được dành nhiều thời gian để làm quen với trẻ. Các bạn nhỏ trong lớp đã bắt đầu quen với việc có chúng tôi và luôn thân thiện, gần gũi với chúng tôi mọi lúc trong lớp học, điều đó đã giúp chúng tôi cảm nhận được tình yêu thương của trẻ dành cho chúng tôi mỗi ngày một lớn. Những ngày đầu tiên trôi qua dù có chút chán nản vì chưa quen công việc mới, môi trường mới nhưng vì sự động viên, quan tâm của các cô giáo chủ nhiệm; nụ cười ngây thơ và sự đáng yêu của các bạn nhỏ, đó là động lực để chúng tôi thích nghi và làm tốt công việc của mình.

Ở tuần thứ 2 chúng tôi thực hiện công tác tập làm chủ nhiệm. Mỗi sáng chúng tôi đến sớm để đón trẻ, sau đó lấy đồ ăn sáng và cho trẻ ăn. Sau khi ăn sáng xong, cho trẻ xuống sân tập thể dục buổi sáng và sau đó quay lại lớp học, hướng dẫn trẻ hoạt động theo kế hoạch hằng ngày mà cô chủ nhiệm lớp đã lên. Mỗi buổi sáng trôi qua thật nhẹ nhàng và vui vẻ.....
Sau những hoạt động buổi sáng của trẻ là giờ ăn trưa, chúng tôi cho trẻ vệ sinh cá nhân sạch sẽ để ngồi vào bàn ăn. Khi ăn xong trẻ vệ sinh sạch sẽ để đi vào phòng ngủ. Sau khi ngủ dậy trẻ ăn chiều và thực hiện các hoạt động chiều cũng như học của các môn năng khiếu như trong thời khóa biểu. Học xong trẻ uống sữa; đến giờ trả trẻ, trẻ nhẹ nhàng đi cất ghế và chào các cô ra về. Mỗi một ngày ở trường trôi qua thật nhanh. Chúng tôi cảm thấy mỗi ngày đến trường của mình thật hạnh phúc, hạnh phúc từ khi trẻ âu yếm chào cô mỗi buổi sáng đến lúc trẻ lễ phép chào cô để ra về mỗi buổi chiều tà. Mỗi một phút giây trôi qua ở bên trẻ thật ý nghĩa làm sao.
Trong tuần thứ 3,4,5,6 của thời gian thực tập chúng tôi cũng đã làm tốt công tác chủ nhiệm lớp của mình. Chúng tôi soạn giáo án và tập dạy đồng thời thực hiện công tác chủ nhiệm lớp. Dường như lúc này chúng tôi đã thân thuộc hơn với các bạn nhỏ nên các bạn cũng quấn quýt chúng tôi nhiều hơn. Ngoài những thời gian của hoạt động học ra, các bạn nhỏ thường xuyên kể cho chúng tôi nghe về những chuyện hằng ngày, những câu chuyện về gia đình,... những câu chuyện dài chẳng có hồi kết.

Tuần thứ 7 của thời gian thực tập, sau khoảng thời gian soạn giáo án, tập giảng thì đây cũng là tuần quan trọng để chúng tôi thực hiện những tiết thi giảng của mình. So với những tuần trước đó thì tuần này chúng tôi cảm thấy áp lực hơn, lo lắng hơn về giờ thi dạy. Tôi còn nhớ rất rõ cái khoảng thời gian này các chị chủ nhiệm lớp tôi đã hỗ trợ và giúp đỡ cho chúng tôi từng li từng tí. Các chị luôn động viên, chia sẻ và luôn tạo cho chúng tôi tâm lý thoải mái nhất có thể để bước vào tiết dạy của mình. Tôi nhớ về cái ngày gần thi dạy của mình, các chị đã thức đến khuya để sửa giúp tôi từng trang giáo án, khi chúng tôi tập giảng các chị đồng hành góp ý để những câu chữ được trau chuốt hơn. Hay là khoảng thời gian gần 12 giờ đêm vẫn cùng chúng tôi trang trí lớp học và chuẩn bị đồ dùng để chúng tôi có một tiết dạy xuất sắc nhất... Những kỷ niệm bên các chị thật đáng nhớ biết bao!
Ở tuần này, chúng tôi vẫn thực hiện công tác chủ nhiệm lớp của mình. Công việc của chúng tôi vẫn diễn ra như mọi ngày. Nhưng những tuần này, chúng tôi cảm thấy nó đặc biệt hơn so với khoảng thời gian đầu, bây giờ các bạn nhỏ đến lớp không chỉ chào chúng tôi bằng những câu nói: “Em chào cô Nhân, Em chào cô Nhi” nữa. Bây giờ mỗi ngày đến lớp các bạn chào chúng tôi bằng những cái ôm thân thiết. Ôi! Cảm xúc thật khó tả! Ước gì thời gian có thể trôi chậm lại. Để chúng tôi mãi được chìm đắm trong những khoảnh khắc yêu thương này.....

Rồi thời gian thực tập của 7 tuần đã trôi qua, khoảng thời gian thực tập tuần cuối cùng cũng đã tới....Bây giờ đây mọi thứ xung quanh chúng tôi trở nên thật thân thuộc. Chúng tôi đã quen với việc mỗi ngày đến trường đều có trẻ để yêu thương, quen với cuộc sống có các cô giáo chủ nhiệm luôn đùm bọc; quen với những lời quan tâm, hỏi han của Ban giám hiệu nhà trường và các cô giáo từ nhà bếp đến các cô giáo của các lớp học thân thương; quen với cảnh bác bảo vệ luôn miệt mài làm việc,... mọi thứ xung quanh đã trở nên quen thuộc.. nhưng chúng tôi buộc phải tạm xa để về trường tiếp tục học tập những môn học còn giang dở của mình.
Bây giờ đây, khi ngồi nghĩ lại khoảng thời gian thực tập, chúng tôi đã mang trong mình thật nhiều cảm xúc đan xen. Thật buồn khi phải xa những bạn nhỏ đáng yêu; xa các cô giáo đã trở nên thân thuộc... Nhưng cũng thật vui vì mỗi chúng tôi đã hoàn thành trọn vẹn nhất kỳ thực tập của mình, 2 tháng qua chúng tôi đã được sống như những giáo viên thực thụ, đã luôn được trẻ yêu thương và là nơi tin tưởng để trẻ gửi gắm những tình cảm chân thành nhất.
Kỳ thực tập tốt nghiệp này chính là cơ hội để chúng tôi được va chạm, trải nghiệm và hoàn thiện hơn bản thân mình, đây cũng là môi trường tốt để chúng tôi có thể thử sức và rèn nghề. Có đi thực tập, thâm nhập vào thực tế thì chúng tôi mới hiểu rõ được năng lực, trình độ, kiến thức mà mình có đến đâu để nhắc nhở bản thân mình phải luôn biết học hỏi và không ngừng phấn đấu để đạt được những gì mình mong muốn.
Hai tháng thực tập ở trường Mầm non Đại Nài đã để lại cho chúng tôi nhiều bài học quý giá và đó sẽ là hành trang quan trọng để chúng tôi mang theo bên mình. Sau này, dù ở bất cứ môi trường nào chúng tôi cũng sẽ luôn cố gắng trau dồi để hoàn thiện bản thân để xứng đáng là những cô giáo mầm non có đủ tâm – trí – lực để đưa những con thuyền cập bến bờ tri thức thành công.




